题目内容
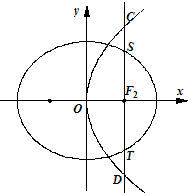 如图,椭圆E:
如图,椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| |CD| |
| |ST| |
| 6 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)设P是椭圆M上的任意一点,EF为圆N:x2+(y-2)2=1的任意一条直径(E、F为直径的两个端点),求
| PE |
| PF |
分析:(Ⅰ)由条件可知椭圆的焦点坐标为(2,0),|CD|=8,|ST|=2•
,利用
=2
可得:2a2=3b4,结合a2=b2+4,即可求得椭圆M的方程;
(2)方法1:设圆N:x2+(y-2)2=1的圆心为N,利用向量的运算,表示出
•
,从而求
•
的最大值转化为求
2的最大值,用坐标表示出
2,即可求得
•
的最大值;
方法2:设点E(x1,y1),F(x2,y2),P(x0,y0),用坐标表示出
•
,利用配方法,即可求得结论;
方法3:分类讨论:直线EF的斜率存在与不垂直,EF的方程与圆的方程联立,用坐标表示出
•
,利用配方法,即可求得结论.
| b2 |
| a |
| |CD| |
| |ST| |
| 6 |
(2)方法1:设圆N:x2+(y-2)2=1的圆心为N,利用向量的运算,表示出
| PE |
| PF |
| PE |
| PF |
| NP |
| NP |
| PE |
| PF |
方法2:设点E(x1,y1),F(x2,y2),P(x0,y0),用坐标表示出
| PE |
| PF |
方法3:分类讨论:直线EF的斜率存在与不垂直,EF的方程与圆的方程联立,用坐标表示出
| PE |
| PF |
解答:解:(Ⅰ)由条件可知椭圆的焦点坐标为(2,0),|CD|=8,|ST|=2•
,
由
=2
可得:2a2=3b4,又a2=b2+4,则3b4-2b2-8=0,解得:b2=2,a2=4,
所以椭圆M的方程为M:
+
=1.…(4分)
(2)方法1:设圆N:x2+(y-2)2=1的圆心为N,
则
•
=(
-
)•(
-
)=(-
-
)•(
-
)=
2-
2=
2-1.
从而求
•
的最大值转化为求
2的最大值.…(6分)
因为P是椭圆M上的任意一点,设P(x0,y0),所以
+
=1,即x02=6-3y02.…(8分)
因为点N(0,2),所以
2=x02+(y0-2)2=-2(y0+1)2+12.…(10分)
因为y0∈[-
,
],所以当y0=-1时,
2取得最大值12.
所以
•
的最大值为11.…(12分)
方法2:设点E(x1,y1),F(x2,y2),P(x0,y0),因为E,F的中点坐标为(0,2),所以
所以
•
=(x1-x0)(x2-x0)+(y1-y0)(y2-y0)=(x1-x0)(-x1-x0)+(y1-y0)(4-y1-y0)
=
-
+
-
+4y1-4y0=
+
-4y0-(
+
-4y1).…(6分)
因为点E在圆N上,所以
+(y1-2)2=1,即
+
-4y1=-3.
因为点P在椭圆M上,所以
+
=1,即
=6-3
.…(10分)
所以
•
=-2
-4y0+9=-2(y0+1)2+11.
因为y0∈[-
,
],所以当y0=-1时,(
•
)max=11.…(12分)
方法3:①若直线EF的斜率存在,设EF的方程为y=kx+2,
由
,解得x=±
.…(6分)
因为P是椭圆M上的任一点,设点P(x0,y0),所以
+
=1,即x02=6-3y02.
所以
=(
-x0,
+2-y0),
=(-
-x0,-
+2-y0)…(8分)
所以
•
=x02-
+(2-y0)2-
=x02+(2-y0)2-1=-2(y0+1)2+11.…(10分)
因为y0∈[-
,
],所以当y0=-1时,
•
取得最大值11.
②若直线EF的斜率不存在,此时EF的方程为x=0,
由
,解得y=1或y=3.
不妨设,E(0,3),F(0,1). 因为P是椭圆M上的任一点,设点P(x0,y0),
所以
+
=1,即x02=6-3y02.所以
=(-x0,3-y0),
=(-x0,1-y0).
所以
•
=x02+y02-4y0+3=-2(y0+1)2+11.
因为y0∈[-
,
],所以当y0=-1时,
•
取得最大值11.
综上可知,
•
的最大值为11.…(12分)
| b2 |
| a |
由
| |CD| |
| |ST| |
| 6 |
所以椭圆M的方程为M:
| x2 |
| 6 |
| y2 |
| 2 |
(2)方法1:设圆N:x2+(y-2)2=1的圆心为N,
则
| PE |
| PF |
| NE |
| NP |
| NF |
| NP |
| NF |
| NP |
| NF |
| NP |
| NP |
| NF |
| NP |
从而求
| PE |
| PF |
| NP |
因为P是椭圆M上的任意一点,设P(x0,y0),所以
| x02 |
| 6 |
| y02 |
| 2 |
因为点N(0,2),所以
| NP |
因为y0∈[-
| 2 |
| 2 |
| NP |
所以
| PE |
| PF |
方法2:设点E(x1,y1),F(x2,y2),P(x0,y0),因为E,F的中点坐标为(0,2),所以
|
所以
| PE |
| PF |
=
| x | 2 0 |
| x | 2 1 |
| y | 2 0 |
| y | 2 1 |
| x | 2 0 |
| y | 2 0 |
| x | 2 1 |
| y | 2 1 |
因为点E在圆N上,所以
| x | 2 1 |
| x | 2 1 |
| y | 2 1 |
因为点P在椭圆M上,所以
| ||
| 6 |
| ||
| 2 |
| x | 2 0 |
| y | 2 0 |
所以
| PE |
| PF |
| y | 2 0 |
因为y0∈[-
| 2 |
| 2 |
| PE |
| PF |
方法3:①若直线EF的斜率存在,设EF的方程为y=kx+2,
由
|
| 1 | ||
|
因为P是椭圆M上的任一点,设点P(x0,y0),所以
| x02 |
| 6 |
| y02 |
| 2 |
所以
| PE |
| 1 | ||
|
| k | ||
|
| PF |
| 1 | ||
|
| k | ||
|
所以
| PE |
| PF |
| 1 |
| k2+1 |
| k2 |
| k2+1 |
因为y0∈[-
| 2 |
| 2 |
| PE |
| PF |
②若直线EF的斜率不存在,此时EF的方程为x=0,
由
|
不妨设,E(0,3),F(0,1). 因为P是椭圆M上的任一点,设点P(x0,y0),
所以
| x02 |
| 6 |
| y02 |
| 2 |
| PE |
| PF |
所以
| PE |
| PF |
因为y0∈[-
| 2 |
| 2 |
| PE |
| PF |
综上可知,
| PE |
| PF |
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查直线与圆的位置关系,正确表示
•
是关键.
| PE |
| PF |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
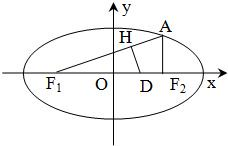 如图,椭圆
如图,椭圆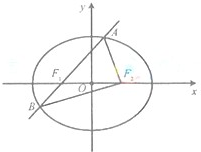 (2012•福建)如图,椭圆E:
(2012•福建)如图,椭圆E: (2013•深圳二模)如图,椭圆E:
(2013•深圳二模)如图,椭圆E: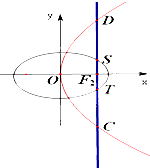 (2012•上高县模拟)如图,椭圆
(2012•上高县模拟)如图,椭圆