题目内容
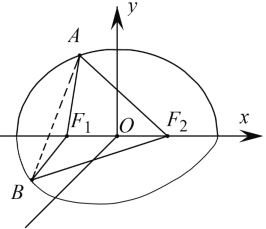
【题目】如图,矩形![]() 中,
中,![]() ,E为边
,E为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() (
(![]() 平面
平面![]() ).若M、O分别为线段
).若M、O分别为线段![]() 、
、![]() 的中点,则在
的中点,则在![]() 翻转过程中,下列说法错误的是( )
翻转过程中,下列说法错误的是( )
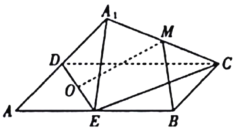
A.与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直;
垂直;
B.异面直线![]() 与
与![]() 所成角是定值;
所成角是定值;
C.一定存在某个位置,使![]() ;
;
D.三棱锥![]() 外接球半径与棱
外接球半径与棱![]() 的长之比为定值;
的长之比为定值;
【答案】C
【解析】
对A,由面面平行可知正确;对B,取![]() 的中点为
的中点为![]() ,作出异面直线所成的角,并证明为定值;对C,利用反证法证明
,作出异面直线所成的角,并证明为定值;对C,利用反证法证明![]() ,与已知矛盾;对D,确定
,与已知矛盾;对D,确定![]() 为三棱锥
为三棱锥![]() 的外接球球心,即可得证.
的外接球球心,即可得证.
取![]() 中点
中点![]() ,连接
,连接![]() .
.![]() 为
为![]() 的中点,
的中点,
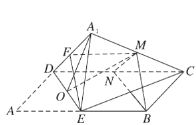
![]() .
.
又![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
![]() .
.![]() ,
,
∴平面![]() 平面
平面![]() 平面
平面![]() ,
,
∴与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直,故A正确.
垂直,故A正确.
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,

则![]() 且
且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角.
所成的角.
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
故异面直线![]() 与
与![]() 所成的角为定值,故B正确.
所成的角为定值,故B正确.
连接![]() .
.![]() 为等腰直角三角形且
为等腰直角三角形且![]() 为斜边
为斜边![]() 中点,
中点,
![]() .若
.若![]() ,则
,则![]() 平面
平面![]() ,
,
![]()
又![]() ,
,
![]() .
.
又![]() 平面
平面![]() ,
,
![]() ,与已知矛盾,故C错误.
,与已知矛盾,故C错误.
![]() ,
,
![]() 为三棱锥
为三棱锥![]() 的外接球球心,又
的外接球球心,又![]() 为定值,故D正确.
为定值,故D正确.
故选:C

 阅读快车系列答案
阅读快车系列答案【题目】2020年1月底因新型冠状病毒感染的肺炎疫情形势严峻,避免外出是减少相互交叉感染最有效的方式.在家中适当锻炼,合理休息,能够提高自身免疫力,抵抗该种病毒.某小区为了调查“宅”家居民的运动情况,从该小区随机抽取了100位成年人,记录了他们某天的锻炼时间,其频率分布直方图如下:
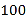
(1)求a的值,并估计这100位居民锻炼时间的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)小张是该小区的一位居民,他记录了自己“宅”家7天的锻炼时长:
序号n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
锻炼时长m(单位:分钟) | 10 | 15 | 12 | 20 | 30 | 25 | 35 |
(Ⅰ)根据数据求m关于n的线性回归方程;
(Ⅱ)若![]() (
(![]() 是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
附;在线性回归方程![]() 中,
中,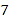 ,
,![]() .
.
【题目】英国“脱欧”这件国际大事引起了社公各界广泛关注,根据最新情况,英国大选之后,预计将会在2020日年1月31日完成“脱欧”,但是因为之前“脱欧”一直被延时,所以很多人认为并不能如期完成,某媒体随机在人群中抽取了100人做调查,其中40岁以下的人群认为能完成的占![]() ,而40岁以上的有10人认为不能完成
,而40岁以上的有10人认为不能完成
(1)完成![]() 列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
能完成 | 不能完成 | 合计 | |
40岁以上 | 55 | ||
40岁以下 | |||
合计 |
(2)现按照分层抽样抽取20人,在这20人的样本中,再选取40岁以下的4人做深度调查,至少有2人认为英国能够完成“脱欧”的概率为多少?
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |