题目内容
【题目】下列说法中正确的是（ ）
A.若两个随机变量的线性相关性越强，则相关系数
的值越接近于1
B.若正态分布
，则
C.把某中学的高三年级560名学生编号：1到560，再从编号为1到10的10名学生中随机抽取1名学生，其编号为
，然后抽取编号为
，
，
，…的学生，这样的抽样方法是分层抽样
D.若一组数据0，，3，4的平均数是2，则该组数据的方差是
【答案】D
【解析】
利用线性相关的强弱与相关系数
的绝对值的关系可判断A；利用正态分布密度曲线的性质可判断B；利用分层抽样的特征可判断C；利用平均数、方差的运算可判断D.
对于A，两个随机变量的线性相关性越强，则相关系数的绝对值越接近于1，故A错误；
对于B，由正态分布
，则正态分布密度曲线关于
对称，
即
，故B错误；
对于C，1到560，再从编号为1到10的10名学生中随机抽取1名学生，
其编号为
，然后等间距抽取编号为
，
，
，…的学生，属于系统抽样，
故C错误；
对于D，一组数据0，，3，4的平均数是2，即
，解得
，
所以方差为
，故D正确.
故选：D
练习册系列答案
相关题目
【题目】某校两个班级100名学生在一次考试中的成绩的频率分布直方图如图所示，其中成绩分组区如下表：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
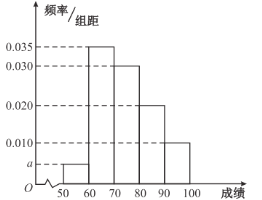
（1）求频率表分布直方图中a的值；
（2）根据频率表分布直方图，估计这100名学生这次考试成绩的平均分；
（3）现用分层抽样的方法从第三、四、五组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率.
