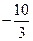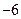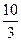题目内容
设向量
,
,
是不共面的三个向量,则下列各组向量不能作为空间向量基底的是( )
| i |
| j |
| k |
A.
| ||||||||||||||||||||||||
B.
| ||||||||||||||||||||||||
C.
| ||||||||||||||||||||||||
D.
|
A.令a
+b
+c
=
,∴a(1,-2,1)+b(-1,3,2)+c(-3,7,0)=(0,0,0),可得
,消去a化为b+c=0,令b=-1,则c=1,a=2.
∴存在一组非0常数a=2,b=-1,c=1使得a
+b
+c
=
,
故
,
,
是共面的三个向量,故不能作为空间向量的基底.
B.令a
+b
+c
=
,即a(1,1,-1)+b(2,3,-5)+c(-7,18,22)=(0,0,0).
可得
,解得a=b=c=0.
故
,
,
是三个不共面的三个向量,可以作为空间向量的基底.
同理C,D可以作为空间向量的基底.
综上可知:只有A不能作为基底.
故选A.
| p |
| q |
| r |
| 0 |
|
∴存在一组非0常数a=2,b=-1,c=1使得a
| p |
| q |
| r |
| 0 |
故
| p |
| q |
| r |
B.令a
| p |
| q |
| r |
| 0 |
可得
|
故
| p |
| q |
| r |
同理C,D可以作为空间向量的基底.
综上可知:只有A不能作为基底.
故选A.

练习册系列答案
相关题目
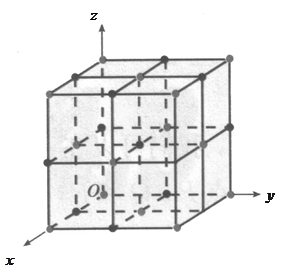
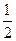 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.如图(2),建立空间直角坐标
的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.如图(2),建立空间直角坐标 后,试写出全部钠原子所在位置的坐标.
后,试写出全部钠原子所在位置的坐标.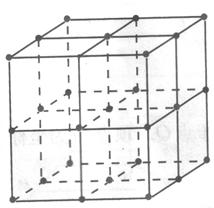
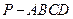 中,底面ABCD是一个平行四边形,
中,底面ABCD是一个平行四边形,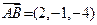 ,
,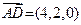 ,
,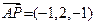
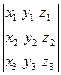 =
=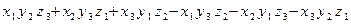 ,对于向量
,对于向量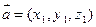 ,
,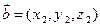 ,
,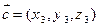 有
有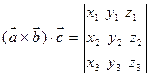 ,
,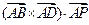 =__________.
=__________. =
=
 ,P是BN上的一点,若
,P是BN上的一点,若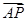 =m
=m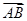 +
+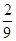
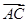 ,则实数m的值为( ).
,则实数m的值为( ).

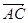 ,
,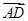 和
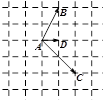
和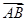 在正方形网格中的位置如图所示,若
在正方形网格中的位置如图所示,若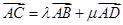 ,则
,则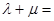 ( )
( )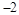
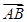 =c,
=c,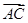 =b.若点D满足
=b.若点D满足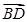 =2
=2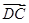 ,则
,则 =________.(用b、c表示)
=________.(用b、c表示)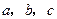 为
为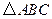 的三个内角
的三个内角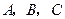 的对边,向量
的对边,向量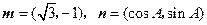 .若
.若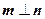 ,且
,且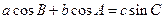 ,则角
,则角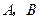 的大小分别为( )
的大小分别为( )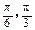
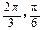
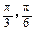
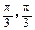
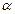 的法向量是
的法向量是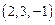 ,平面
,平面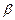 的法向量是
的法向量是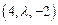 ,若
,若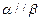 ,则
,则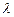 的值是( )
的值是( )