题目内容
11.函数y=x$\sqrt{1-{x}^{2}}$的最大值为$\frac{1}{2}$.分析 根据基本不等式的性质解答即可.
解答 解:x<0时,y<0,x>0时,y>0,
显然函数y=x$\sqrt{1-{x}^{2}}$取得最大值时,x>0,
而x>0时,y=x$\sqrt{1-{x}^{2}}$=$\sqrt{{x}^{2}(1{-x}^{2})}$≤$\sqrt{{(\frac{{x}^{2}+1{-x}^{2}}{2})}^{2}}$=$\sqrt{{(\frac{1}{2})}^{2}}$=$\frac{1}{2}$,
当且仅当x2=1-x2,即x=$\frac{\sqrt{2}}{2}$时“=”成立,
故答案为:$\frac{1}{2}$.
点评 本题考查了基本不等式的性质,考查函数的最值问题,是一道基础题.

练习册系列答案
相关题目
1.tan75°=( )
| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | 2-$\sqrt{3}$ |
2.已知函数f(x)在R上可导,下列四个选项中正确的是( )
| A. | 若f(x)>f′(x)对x∈R恒成立,则 ef(1)<f(2) | |
| B. | 若f(x)<f′(x)对x∈R恒成立,则e2f(-1)>f(1) | |
| C. | 若f(x)+f′(x)>0对x∈R恒成立,则ef(2)<f(1) | |
| D. | 若f(x)+f′(x)<0对x∈R恒成立,则f(-1)>e2f(1) |
6.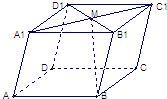 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{BM}$相等的向量是( )
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{BM}$相等的向量是( )
 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{BM}$相等的向量是( )
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{BM}$相等的向量是( )| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
16.某人在C点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D点测得塔顶A的仰角为30°,则塔高为( )
| A. | 15米 | B. | 5米 | C. | 10米 | D. | 12米 |
3.一元二次不等式x2+2x-15>0的解集是( )
| A. | {x|-5<x<3} | B. | {x|x<-5或x>3} | C. | {x|-3<x<5} | D. | {x|x<-3或x>-5} |
 如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20152的格点的坐标为(1008,1007).
如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20152的格点的坐标为(1008,1007).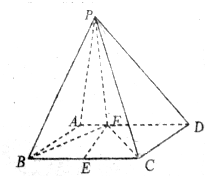 如图,四棱锥P-ABCD的地面ABCD是平行四边形,PF⊥平面ABCD,垂足F在AD上,且AF=$\frac{1}{3}$FD,FB⊥FC,FB=FC=2,PF=4,E是BC的中点.
如图,四棱锥P-ABCD的地面ABCD是平行四边形,PF⊥平面ABCD,垂足F在AD上,且AF=$\frac{1}{3}$FD,FB⊥FC,FB=FC=2,PF=4,E是BC的中点.