题目内容
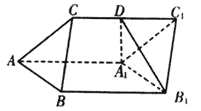
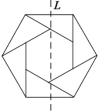
【题目】如图，已知六个直角边均为1和
的直角三角形围成的两个正六边形，则该图形绕着
旋转一周得到的几何体的体积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
根据图形，外面的六边形的边长为
，旋转得到的几何体是两个同底的圆台，再根据圆台的体积公式求解，内部的六边形边长为1，旋转得到的几何体是一个圆柱，两个与圆柱同底的圆锥.再根据圆柱，圆锥的体积公式求解，然后外部的减内部的体积即为所求.
根据题意，外面的六边形边长为，
旋转得到的几何体是两个同底的圆台，
上底半径为
，下底半径为，高为
，
所以旋转得到的几何体的体积为
，内部的六边形边长为1
旋转得到的几何体是一个圆柱，两个与圆柱同底的圆锥，
圆锥的底面半径为，高为
，圆柱的底面半径为，高为1，
内部的六边形旋转得到的几何体的体积为
，
所以几何体的体积为
.
故选：B
练习册系列答案
名校课堂系列答案
相关题目
【题目】某中学为了解高二年级中华传统文化经典阅读的整体情况，从高二年级随机抽取10名学生进行了两轮测试，并把两轮测试成绩的平均分作为该名学生的考核成绩.记录的数据如下：
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | |
第一轮测试成绩 | 96 | 89 | 88 | 88 | 92 | 90 | 87 | 90 | 92 | 90 |
第二轮测试成绩 | 90 | 90 | 90 | 88 | 88 | 87 | 96 | 92 | 89 | 92 |
（Ⅰ）从该校高二年级随机选取一名学生，试估计这名学生考核成绩大于90 分的概率；
（Ⅱ）从考核成绩大于90分的学生中再随机抽取两名同学，求这两名同学两轮测试成绩均大于等于90分的概率；
（Ⅲ）记抽取的10名学生第一轮测试的平均数和方差分别为
，
，考核成绩的平均数和方差分别为
，
，试比较与， 与的大小.（只需写出结论）