题目内容
【题目】某中学为了解高二年级中华传统文化经典阅读的整体情况,从高二年级随机抽取10名学生进行了两轮测试,并把两轮测试成绩的平均分作为该名学生的考核成绩.记录的数据如下:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | |
第一轮测试成绩 | 96 | 89 | 88 | 88 | 92 | 90 | 87 | 90 | 92 | 90 |
第二轮测试成绩 | 90 | 90 | 90 | 88 | 88 | 87 | 96 | 92 | 89 | 92 |
(Ⅰ)从该校高二年级随机选取一名学生,试估计这名学生考核成绩大于90 分的概率;
(Ⅱ)从考核成绩大于90分的学生中再随机抽取两名同学,求这两名同学两轮测试成绩均大于等于90分的概率;
(Ⅲ)记抽取的10名学生第一轮测试的平均数和方差分别为![]() ,
,![]() ,考核成绩的平均数和方差分别为
,考核成绩的平均数和方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() ,
, ![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() ,
, ![]() .
.
【解析】分析:(Ⅰ)求出这![]() 名学生两轮考核的平均成绩,可知大于等于
名学生两轮考核的平均成绩,可知大于等于![]() 分的有6人,利用古典概型概率公式可得结果;(Ⅱ)由(Ⅰ)知,考核成绩大于等于90分的学生共6人,其成绩均大于等于
分的有6人,利用古典概型概率公式可得结果;(Ⅱ)由(Ⅰ)知,考核成绩大于等于90分的学生共6人,其成绩均大于等于![]() 分共3人,利用列举法可得
分共3人,利用列举法可得![]() 人中选两人的事件有
人中选两人的事件有![]() 个事件,其中这两名同学两轮测试成绩均大于等于
个事件,其中这两名同学两轮测试成绩均大于等于![]() 分的事件有
分的事件有![]() 个,由古典概型概率公式可得结果;(Ⅲ)根据成绩的平均值以及成绩的稳定性可得结果.
个,由古典概型概率公式可得结果;(Ⅲ)根据成绩的平均值以及成绩的稳定性可得结果.
详解:(Ⅰ)这10名学生的考核成绩(单位:分)分别为:
93,89.5,89,88,90,88.5,91.5,91,90.5,91.
其中大于等于90分的有1号、5号、7号、8号、9号、10号,共6人.
所以样本中学生考核成绩大于等于90分的频率是![]() .
.
从该校高二年级随机选取一名学生,估计这名学生考核成绩大于等于90分的概率为0.6.
(Ⅱ)设事件![]() 为“从考核成绩大于等于90分的学生中任取2名同学,这2名同学两轮测试成绩均大于等于90分”,
为“从考核成绩大于等于90分的学生中任取2名同学,这2名同学两轮测试成绩均大于等于90分”,
由(Ⅰ)知,考核成绩大于等于90分的学生共6人,其中两轮测试成绩均大于等于90分的学生有1号,8号,10号,共3人.
因此,从考核成绩大于等于90分的学生中任取2名同学,
包含(1号,5号)、(1号,7号)、(1号,8号)、(1号,9号)、(1号、10号)、
(5号,7号)、(5号,8号)、(5号,9号)、(5号,10号)、(7号,8号)、(7号,9号)、(7号,10号)、(8号,9号)、(8号,10号)、(9号,10号)共15个基本事件,
而事件![]() 包含(1号,8号)、(1号、10号)、(8号,10号)共3个基本事件,
包含(1号,8号)、(1号、10号)、(8号,10号)共3个基本事件,
所以![]() .
.
(Ⅲ)![]() ,
, ![]() .
.

【题目】在衡阳市“创全国文明城市”(简称“创文”)活动中,市教育局对本市A,B,C,D四所高中学校按各校人数分层抽样,随机抽查了200人,将调查情况进行整理后制成下表:
学校 | A | B | C | D |
抽查人数 | 10 | 15 | 100 | 75 |
“创文”活动中参与的人数 | 9 | 10 | 80 | 49 |
假设每名高中学生是否参与“创文”活动是相互独立的
(1)若本市共8000名高中学生,估计C学校参与“创文”活动的人数;
(2)在上表中从A,B两校没有参与“创文”活动的同学中随机抽取2人,求恰好A,B两校各有1人没有参与“创文”活动的概率;
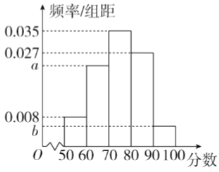
(3)在随机抽查的200名高中学生中,进行文明素养综合素质测评(满分为100分),得到如上的频率分布直方图,其中![]() .求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
.求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).