��Ŀ����
20����֪�ڡ�ABC�У���A��B��C�ɹ������0�ĵȲ����У�������������1-cos2A-cos2C+cos2Acos2C=$\frac{4+2\sqrt{3}}{4}$����$\frac{a+\sqrt{2}b}{c}$��ֵΪ��������| A�� | $\frac{\sqrt{6}+1}{2}$ | B�� | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C�� | $\frac{2+\sqrt{3}}{4}$ | D�� | 2 |
���� ������ɵý�ã�A��B��C��B=$\frac{��}{3}$�����������ɵ�sinAsinC=$\frac{\sqrt{3}+1}{4}$�����ɻ����Ͳʽ�ɵ�cos��-A+C��=$\frac{\sqrt{3}}{2}$����C-A=30�㣬�ɴ˿ɵ� A��C��ֵ�����sinA��sinB ��ֵ�����������Ǻ͵����ҹ�ʽ���sinC��ֵ���������Ҷ���������ֵ��
��� �⣺���ڡ�ABC�У���A��B��C�ɹ������0�ĵȲ����У�2B=A+C��A+B+C=�У�
���ã�A��B��C��B=$\frac{��}{3}$��
��1-cos2A-cos2C+cos2Acos2C=$\frac{4+2\sqrt{3}}{4}$��
��ɵã���1-cos2A����1-cos2C��=$\frac{4+2\sqrt{3}}{4}$��
��2sin2A•2sin2C=$\frac{4+2\sqrt{3}}{4}$����sin2A•sin2C=��$\frac{\sqrt{3}+1}{4}$��2��
�ɵã�sinAsinC=$\frac{\sqrt{3}+1}{4}$
���ã�-$\frac{1}{2}$[cos��A+C��-cos��A-C��]=$\frac{\sqrt{3}+1}{4}$��
��ã�cos��A-C��=$\frac{\sqrt{3}}{2}$��
��C-A=$\frac{��}{6}$����ã�A=$\frac{��}{4}$��C=$\frac{5��}{12}$
��sinA=$\frac{\sqrt{2}}{2}$��sinB=$\frac{\sqrt{3}}{2}$��sinC=sin��$\frac{��}{4}+\frac{��}{6}$��=$\frac{\sqrt{6}+\sqrt{2}}{4}$
��$\frac{a+\sqrt{2}b}{c}$=$\frac{sinA+\sqrt{2}sinB}{sinC}$=$\frac{\frac{\sqrt{2}}{2}+\sqrt{2}��\frac{\sqrt{3}}{2}}{\frac{\sqrt{6}+\sqrt{2}}{4}}$=2��
���� ������Ҫ�������Ǻ����ĺ�ȱ任��������ֵ���Ȳ����еĶ�������ʣ����Ҷ�����Ӧ�ã������е���

 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�| A�� | y=sinx | B�� | y=cosx | C�� | y=sin2x | D�� | y=cos2x |
| A�� | x=$\frac{��}{2}$+1 | B�� | x=$\frac{��}{2}$ | C�� | x=��+1 | D�� | x=�� |
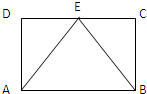 ��ͼ������ABCD�У���EΪ��CD���е㣬���ھ���ABCD�ڲ������ȡһ����Q�����Qȡ�ԡ�ABE�ڲ��ĸ��ʵ��ڣ�������
��ͼ������ABCD�У���EΪ��CD���е㣬���ھ���ABCD�ڲ������ȡһ����Q�����Qȡ�ԡ�ABE�ڲ��ĸ��ʵ��ڣ�������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{1}{2}$ |
 ��ֱ֪����Ǧ�-l-�£���A�ʦ���AC��l��CΪ���㣬��B�ʦ���BD��l��DΪ���㣬��AB=2��AC=BD=1����D��ƽ��ABC�ľ��룮
��ֱ֪����Ǧ�-l-�£���A�ʦ���AC��l��CΪ���㣬��B�ʦ���BD��l��DΪ���㣬��AB=2��AC=BD=1����D��ƽ��ABC�ľ��룮