题目内容
11.已知SC是三棱锥S-ABC外接球直径,SC=2,AB=BC=AC=1,则三棱锥体积为多少.分析 根据题意作出图形,利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积.
解答 解:根据题意作出图形: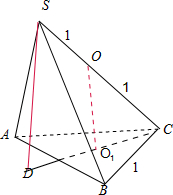
设球心为O,过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
延长CO1交球于点D,则SD⊥平面ABC.
∵CO1=$\frac{2}{3}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$,
∴OO1=$\sqrt{{1}^{2}-(\frac{\sqrt{3}}{3})^{2}}$=$\frac{\sqrt{6}}{3}$,
∴高SD=2OO1=$\frac{2\sqrt{6}}{3}$,
∵△ABC是边长为1的正三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}$,
∴V三棱锥S-ABC=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{2\sqrt{6}}{3}$=$\frac{\sqrt{2}}{6}$.
点评 本题考查三棱锥体积,考查学生的计算能力,利用截面圆的性质求出OO1是解题的关键.

练习册系列答案
相关题目
1.过点A(4,y),B(2,-3)的直线的倾斜角为135°,则y等于( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
2.某几何体的三视图如图所示,则其表面积为( )


| A. | $\frac{\sqrt{5}π}{2}$+2 | B. | $\frac{\sqrt{5}+1}{2}π+\sqrt{3}$ | C. | $\frac{\sqrt{5}π}{2}+\sqrt{3}$ | D. | $\frac{\sqrt{5}+1}{2}π+2$ |
6.设$\frac{3}{2}$π<α<2π,则$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cos2α}}$=( )
| A. | -cos$\frac{α}{2}$ | B. | cos$\frac{α}{2}$ | C. | sin$\frac{α}{2}$ | D. | -sin$\frac{α}{2}$ |
20.已知在△ABC中,角A、B、C成公差大于0的等差数列,且满足条件:1-cos2A-cos2C+cos2Acos2C=$\frac{4+2\sqrt{3}}{4}$,则$\frac{a+\sqrt{2}b}{c}$的值为( )
| A. | $\frac{\sqrt{6}+1}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{2+\sqrt{3}}{4}$ | D. | 2 |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.