如图.矩形ABCD中.点E为边CD的中点.若在矩形ABCD内部随机抽取一个点Q.则点Q取自△ABE内部的概率等于( )A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

6．

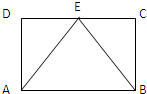如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机抽取一个点Q，则点Q取自△ABE内部的概率等于（　　）

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{2}{3}$

D．

$\frac{1}{2}$

分析利用几何概型的计算概率的方法解决本题，关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积，通过相除的方法完成本题的解答

解答解：由几何概型的计算方法，
可以得出所求事件的概率为P=$\frac{{S}_{△ABC}}{{S}_{矩形ABCD}}$=$\frac{1}{2}$．
故选：D

点评本题主要考查了几何概型，解决此类问题的关键是弄清几何测度，属于基础题．

练习册系列答案

$\frac{\sqrt{6}+1}{2}$

B．

$\frac{\sqrt{6}+\sqrt{2}}{4}$

C．

$\frac{2+\sqrt{3}}{4}$

D．

17．在△ABC中，若（2a-c）tanC=ctanB，求B．

14．一个等比数列的第3项和第4项分别是12和18，则它的第1项与第2项的和为（　　）

1．在△ABC中，A、B、C所对的边分别是a、b、c，若$\overrightarrow{m}$=（b，3a），$\overrightarrow{n}$=（c，b），且$\overrightarrow{m}$∥$\overrightarrow{n}$，C-A=$\frac{π}{2}$，求B．

11．已知{a_n}（n∈N⁺）是各项为正数的等比数列，q是其公比，T_n是前n项的积，且T₅＜T₆，T₆=T₇＞T₈，则下列判断正确的是（　　）

0＜a₆a₈＜1

T₉＜T₅

18．在△ABC中，已知a²-（b²-c²）=（2-$\sqrt{3}$）bc，sinA•sinB=cos²$\frac{C}{2}$，
（1）求角A，角B；
（2）求sinB•sinC的值．

15．试求与圆C₁：（x-1）²+y²=1相外切，且与直线x+$\sqrt{3}$y=0相切于点Q（3，-$\sqrt{3}$）的圆的方程．

16．已知数列{a_n}的前n项和为S_n，且满足a₁=-2，a_n+1+3S_n+2=0（n∈N^*）．
（1）求a₂、a₃的值；
（2）求数列{a_n}的通项公式；
（3）是否存在整数对（m、n），使得等式a_n²-m•a_n=4m+8成立？若存在，请求出所有满足条件的（m，n）；若不存在，请说明理由．

试题分类