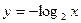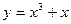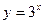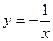题目内容
(本小题满分14分)
已知:函数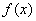 是定义在
是定义在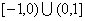 上的偶函数,当
上的偶函数,当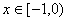 时,
时,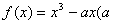 为实数).
为实数).
(1)当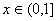 时,求
时,求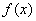 的解析式;
的解析式;
(2)若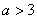 ,试判断
,试判断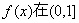 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)是否存在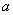 ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出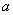 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知:函数
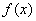 是定义在
是定义在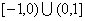 上的偶函数,当
上的偶函数,当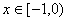 时,
时,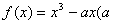 为实数).
为实数).(1)当
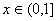 时,求
时,求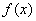 的解析式;
的解析式;(2)若
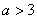 ,试判断
,试判断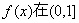 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;(3)是否存在
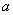 ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出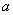 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)
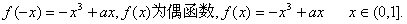
(2)
 上为增函数.
上为增函数.(3)存在
 上有最大值1.
上有最大值1.解:
(I)设
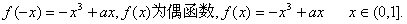
(II)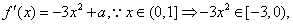
又 上为增函数.
上为增函数.
(III)当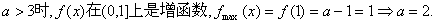 不合题意,舍去)
不合题意,舍去)
当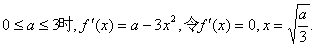 如下表:
如下表:

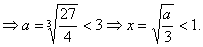
当 无最大值.
无最大值.
∴存在 上有最大值1.
上有最大值1.
(I)设

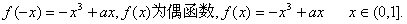
(II)
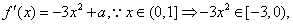
又
 上为增函数.
上为增函数.(III)当
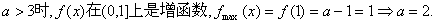 不合题意,舍去)
不合题意,舍去)当
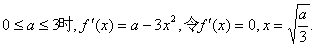 如下表:
如下表:| x[ |  | 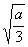 | 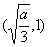 |
 | + | 0 | - |
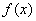 |  | 最大值 |  [ [ |

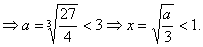
当
 无最大值.
无最大值.∴存在
 上有最大值1.
上有最大值1.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
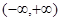 上的偶函数
上的偶函数 满足
满足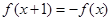 ,且
,且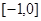 上是增函数,下面五个关于
上是增函数,下面五个关于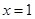 对称;③
对称;③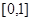 上是增函数;④
上是增函数;④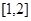 上为减函数;⑤
上为减函数;⑤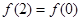 ,正确命题的个数是 ( )
,正确命题的个数是 ( )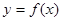 在区间[3,7]上是增函数,且最小值为-5,那么
在区间[3,7]上是增函数,且最小值为-5,那么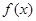 在区间[-7,-3]
在区间[-7,-3]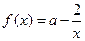 .
.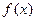 的奇偶性;
的奇偶性; 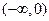 上的单调性并用定义证明.
上的单调性并用定义证明.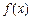 为定
为定 义在R上的奇函数,当
义在R上的奇函数,当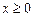 时,
时,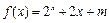 (
(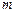 为常数),则
为常数),则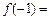

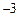
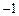
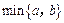 表示a,b两数中的较小数. 设函数
表示a,b两数中的较小数. 设函数 的图象关于直线
的图象关于直线 对称,则t的值为 ▲ .
对称,则t的值为 ▲ .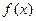 和偶函数
和偶函数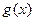 满足
满足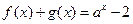 ,
,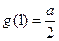 ,则
,则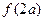 等于 .
等于 . 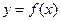 与
与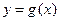 有相同的定义域,且都不是常值函数,对于定义域
有相同的定义域,且都不是常值函数,对于定义域 内的任何
内的任何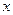 , 有
, 有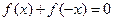 ,
, ,且当
,且当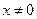 时,
时, ,则
,则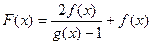 的奇偶性为 ( )
的奇偶性为 ( )