题目内容
设 和
和 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 平行于
平行于 ;
;
(2)若 外一条直线
外一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 和
和 平行;
平行;
(3)设 和
和 相交于直线
相交于直线 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 和
和 垂直;
垂直;
(4)直线 与
与 垂直的充分必要条件是
垂直的充分必要条件是 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
(1)(2).
解析试题分析:一个平面内两条相交直线与另一个平面的两条直线平行则这两条相交直线与平面平行,所以(1)是正确的.平面外一条直线与平面内一条直线平行则这条直线平行于这个平面这是直线与平面平行的判定定理.所以(2)正确.平面内一条直线垂直与这个平面与另一平面的交线不能得到这两平面垂直.所以(3)不正确.直线与平面垂直的充要条件是这条直线垂直于平面内两条相交直线.所以(4)不正确.本题的解题关键是记清各种判断定理,才能正确解题.
考点:1.面面平行.2.直线与平面平行.3.面面垂直.4.直线与平面垂直.

练习册系列答案
相关题目
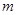 、
、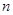 表示不同的直线,
表示不同的直线,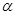 ,
,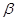 ,
,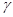 表示不同的平面,则下列四个命题正确的是 .
表示不同的平面,则下列四个命题正确的是 .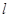 ,且
,且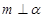 ,则
,则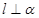 ;②若
;②若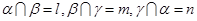 ,则
,则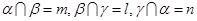 ,且
,且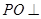 平面
平面 ,垂足为
,垂足为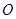 ,直线
,直线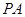 是平面
是平面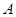 ,其中
,其中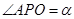 ,过点
,过点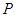 的动直线
的动直线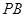 交平面
交平面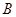 ,
,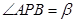 ,则下列说法正确的是___________.
,则下列说法正确的是___________.
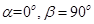 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;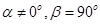 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;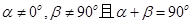 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;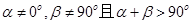 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;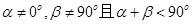 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.
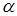 和
和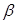 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题: 与
与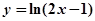 上的点到直线
上的点到直线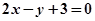 的最短距离是____________
的最短距离是____________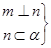 ⇒m⊥α;②
⇒m⊥α;②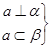 ⇒α⊥β;
⇒α⊥β;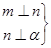 ⇒m∥n;④
⇒m∥n;④ ⇒m∥n
⇒m∥n