Question

【题目】如图，已知P（x0 ， y0）是椭圆C： =1上一点，过原点的斜率分别为k1 ， k2的两条直线与圆（x﹣x0）2+（y﹣y0）2= 均相切，且交椭圆于A，B两点．

（1）求证：k1k2=﹣ ；
（2）求|OA||OB|得最大值．

Answer 1

【答案】
（1）

证明：由圆P与直线OA：y=k1x相切，

可得 = ，

即（4﹣5x02）k12+10x0y0k1+4﹣5y02=0，

同理，（4﹣5x02）k22+10x0y0k2+4﹣5y02=0，

即有k1，k2是方程（4﹣5x02）k2+10x0y0k+4﹣5y02=0的两根，

可得k1k2= = =﹣

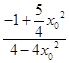（2）

解：设A（x1，y1），B（x2，y2），联立 ，

解得x12= ，y12= ，

同理，x22= ，y22= ，

（|OA||OB|）2=（ + ）（ + ），

∴|OA||OB|=2

=2 ≤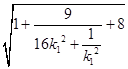

当且仅当k1=± 时，取等号，

可得|OA||OB|的最大值为

【解析】（1）推导出k1 ， k2是方程（4﹣5x02）k2+10x0y0k+4﹣5y02=0的两根，由此能利用韦达定理能求出k1k2为定值；（2）设A（x1 ， y1），B（x2 ， y2），联立 ，由此利用椭圆性质，结合已知条件运用基本不等式能求出|OA||OB|的最大值．
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案，需要熟知椭圆标准方程焦点在x轴：，焦点在y轴：．