题目内容
【题目】已知函数f(x)=|xex+1|,关于x的方程f2(x)+2sinαf(x)+cosα=0有四个不等实根,sinα﹣cosα≥λ恒成立,则实数λ的最大值为( )
A.﹣ ![]()
B.﹣ ![]()
C.﹣ ![]()
D.﹣1
【答案】A
【解析】解:f(x)=|xex+1|= 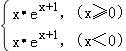 ,当x≥0时,f′(x)=ex+1+xex+1≥0恒成立,所以f(x)在[0,+∞)上为增函数;
,当x≥0时,f′(x)=ex+1+xex+1≥0恒成立,所以f(x)在[0,+∞)上为增函数;
当x<0时,f′(x)=﹣ex+1﹣xex+1=﹣ex+1(x+1),
由f′(x)=0,得x=﹣1,当x∈(﹣∞,﹣1)时,f′(x)=﹣ex+1(x+1)>0,f(x)为增函数,
当x∈(﹣1,0)时,f′(x)=﹣ex+1(x+1)<0,f(x)为减函数,
所以函数f(x)=|xex+1|的极大值为f(﹣1)=|(﹣1)e0|=1,
极小值为:f(0)=0,
令f(x)=m,由韦达定理得:m1+m2=﹣2sinα,m1m2=cosα,
此时若sinα>0,则当m1<0,且m2<0,
此时方程f2(x)+2sinαf(x)+cosα=0至多有两个实根,
若sinα<0,则当m1>0,且m2>0,
要使方程f2(x)+2sinαf(x)+cosα=0有四个实数根,
则方程m2+2sinαm+cosα=0应有两个不等根,
且一个根在(0,1)内,一个根在(1,+∞)内,
再令g(m)=m2+2sinαm+cosα,
因为g(0)=cosα>0,①
△=4sin2α﹣4cosα>0,则1﹣cos2α﹣cosα>0,②
则只需g(1)<0,即1+2sinα+cosα<0,
所以0<cosα<﹣1﹣2sinα,③
由①②解得:0<cosα< ![]() ,④
,④
由③④得到:sinα< ![]() ,
, ![]() <cosα<
<cosα< ![]() ,
,
所以sinα﹣cosα< ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,
,
∴λ≤﹣ ![]() .
.
故选:A.

 一课一练课时达标系列答案
一课一练课时达标系列答案
