题目内容
【题目】若函数![]() 满足:在区间
满足:在区间![]() 内有且仅有一个实数
内有且仅有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质M.
具有性质M.
![]() 判断函数
判断函数![]() 是否具有性质M,说明理由;
是否具有性质M,说明理由;
![]() 若函数
若函数![]() 具有性质M,求实数a的取值范围;
具有性质M,求实数a的取值范围;
![]() 若函数
若函数![]() 具有性质M,求实数m的取值范围.
具有性质M,求实数m的取值范围.
【答案】(1)具有;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)验证![]() 在
在![]() 上是否有唯一解即可.
上是否有唯一解即可.
(2)令![]() 可得
可得![]() ,依据定义有
,依据定义有![]() ,结合
,结合![]() 且
且![]() 可得实数
可得实数![]() 的取值范围.
的取值范围.
(3)构建新函数![]() ,根据
,根据![]() 在
在![]() 上有唯一解可以得到
上有唯一解可以得到![]() 或
或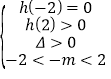 或
或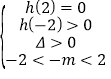 或
或![]() ,解不等式组可得实数
,解不等式组可得实数![]() 的取值范围.
的取值范围.
(1)令![]() ,可得
,可得![]() ,故函数
,故函数![]() 具有性质
具有性质![]() ;
;
(2)因为函数![]() (
(![]() )具有性质
)具有性质![]() ,
,
故![]() ,即
,即![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() ;
;
(3)依题意,若函数![]() 具有性质
具有性质![]() ,
,
即方程![]() 在
在![]() 上有且只有一个实根.
上有且只有一个实根.
设![]() ,故
,故![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
若![]() 即
即![]() ,解得
,解得![]() 或
或![]() .
.
②若![]() ,解得
,解得![]() ;
;
③若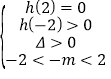 ,解得
,解得![]() ;
;
④若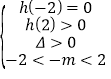 ,无解
,无解
综上所述,若函数![]() 具有性质
具有性质![]() ,实数
,实数![]() 的取值范围是
的取值范围是![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目