题目内容
12.根据下列条件.求α的其他三角函数值:(1)sinα=-$\frac{\sqrt{3}}{2}$,且α是第四象限的角;
(2)tanα=-3,且α是第二象限的角;
(3)cosα=$\frac{12}{13}$,且α是第四象限的角;
(4)sinα=-$\frac{1}{2}$,且α是第三象限的角.
分析 根据同角三角函数基本关系的运用,再根据已知确定三角函数值的符号即可进行求解.
解答 解:(1)∵sinα=-$\frac{\sqrt{3}}{2}$,α是第四象限的角,
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{1}{2}$,tanα=$\frac{sinα}{cosα}$=-$\sqrt{3}$;
(2)∵tanα=-3,且α是第二象限的角,
∴cosα=-$\sqrt{\frac{1}{1+ta{n}^{2}α}}$=-$\frac{\sqrt{10}}{10}$,sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{3\sqrt{10}}{10}$;
(3)∵cosα=$\frac{12}{13}$,且α是第四象限的角,
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{5}{13}$,tan$α=\frac{sinα}{cosα}$=-$\frac{5}{12}$;
(4)∵sinα=-$\frac{1}{2}$,且α是第三象限的角,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{\sqrt{3}}{2}$,tan$α=\frac{sinα}{cosα}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了三角函数同角的平方关系的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
2.己知f(x)=2sin(x+$\frac{π}{3}$)(x∈R),函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
7.有下列说法:①-2是16的四次方根;②正数的n次方根有两个;③a的n次方根就是$\root{n}{a}$;④$\root{n}{{a}^{n}}$=a(a≥0),其中正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
4.已知集合A={x|2x2+3x-2<0},集合B={x|x>a},如果“x∈A”是“x∈B”的充分不必要条件,则实数a的取值范围是( )
| A. | a≤-2 | B. | a<-2 | C. | a>-2 | D. | a≥-2 |
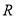 的函数
的函数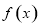 满足下列条件:①对任意的实数
满足下列条件:①对任意的实数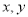 都有:
都有: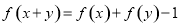 ;②当
;②当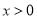 时,
时,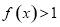 .
.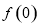 ;
;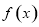 在
在 上为增函数;
上为增函数;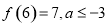 ,关于
,关于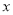 的不等式
的不等式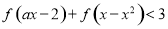 对任意
对任意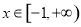 恒成立,求实数
恒成立,求实数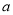 的取值范围.
的取值范围.