题目内容
6.数列{an}满足a1=1,an+1=an+n+1(n∈N•),则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$等于( )| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{1008}$ | D. | $\frac{1007}{1008}$ |
分析 由所给的式子得an+1-an=n+1,给n具体值列出n-1个式子,再他们加起来,求出an,再用裂项法求出$\frac{1}{{a}_{n}}$,然后代入$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$求值.
解答 解:∵an+1=an+n+1(n∈N•),∴an+1-an=n+1,
∴a2-a1=1+1,
a3-a2=2+1,
a4-a3=3+1,
…
an-an-1=(n-1)+1,
以上等式相加,得an-a1=1+2+3+…+(n-1)+n-1,
把a1=1代入上式得,an=1+2+3+…+(n-1)+n=$\frac{n(n+1)}{2}$,
∴$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}-\frac{1}{n+1}$),
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$=2[(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{2015}-\frac{1}{2016}$)]
=2(1-$\frac{1}{2016}$)
=$\frac{2015}{1008}$.
故选:C.
点评 本题考查数列的前n项倒数和的求法,是中档题,解题时要注意累加法和裂项求和法的合理运用.

练习册系列答案
相关题目
11.化简:lg2•lg50+${3}^{{2log}_{3}(lg5)}$=( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |

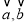 ,满足
,满足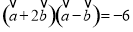 ,且
,且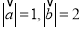 ,则
,则 与
与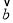 的夹角为( )
的夹角为( )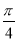 B.
B.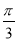 C.
C.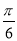 D.
D.