题目内容
9.已知二次函数f(x)满足f(0)=0且f(x+1)=f(x)+x+1,g(x)=2f(-x)+x.求:(1)f(x)的表达式;
(2)f(g(x))的表达式.
分析 (1)设出二次函数的一般形式后,代入f(0)=0且f(x+1)=f(x)+x+1,化简后根据多项式相等的条件求出a,b及c的值,即可确定出f(x)的解析式;
(2)确定g(x),即可求出f(g(x))的表达式.
解答 解:(1)令f(x)=ax2+bx+c(a≠0)
∵f(0)=0,
∴c=0,
∴f(x)=ax2+bx
∵f(x+1)=f(x)+x+1,
∴a(x+1)2+b(x+1)-(ax2+bx)=x+1,
∴2ax+a+b=x+1,即2a=1,a+b=1,
∴a=$\frac{1}{2}$,b=$\frac{1}{2}$,
∴f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x;
(2)g(x)=2f(-x)+x=2($\frac{1}{2}$x2-$\frac{1}{2}$x)+x=x2,
∴f(g(x))=$\frac{1}{2}$x4+$\frac{1}{2}$x2.
点评 此题考查学生会利用待定系数法求函数的解析式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
2.己知f(x)=2sin(x+$\frac{π}{3}$)(x∈R),函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
4.已知集合A={x|2x2+3x-2<0},集合B={x|x>a},如果“x∈A”是“x∈B”的充分不必要条件,则实数a的取值范围是( )
| A. | a≤-2 | B. | a<-2 | C. | a>-2 | D. | a≥-2 |
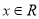 ,则“
,则“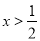 ”是“
”是“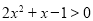 ”的( )
”的( )