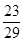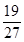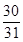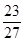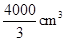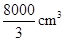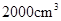题目内容
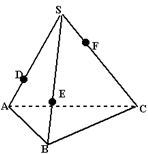
如图,四棱锥S—ABCD的底面为正方形,SD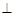 底面ABCD,则下列结论中不正确的是
底面ABCD,则下列结论中不正确的是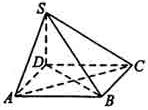
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
D
解析试题分析:设BD、AC相较于点O,
因为SD⊥底面ABCD,底面ABCD为正方形,所以连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;
因为AB∥CD,AB?平面SCD,CD?平面SCD,所以AB∥平面SCD,故B正确;
因为SD⊥底面ABCD,∠ASO是SA与平面SBD所成的角,∠DSO是SC与平面SBD所成的,而△SAO≌△CSO,所以∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;
∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,而这两个角显然不相等,故D不正确;故选D.
考点:线面垂直的判定定理;线面垂直的性质定理;线面平行的判断定理;线面角;异面直线所成的角。
点评:此题考查的知识点较多,综合性强,是个中档题.做本题的关键是熟练掌握线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角等问题,.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
半径为15 cm,圆心角为216°的扇形围成圆锥的侧面,则圆锥的高是( )
| A.14 cm | B.12 cm | C.10 cm | D.8 cm |
已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )
| A.1 | B. | C. | D.2 |
将边长为1的正方形ABCD,沿对角线AC折起,使BD=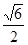 .则三棱锥D-ABC的体积为( )
.则三棱锥D-ABC的体积为( )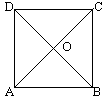
A.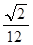 | B.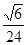 | C. | D.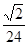 |
设四棱锥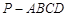 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面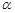 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面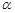 ( )
( )
| A.不存在 | B.有且只有1个 | C.恰好有4个 | D.有无数多个 |

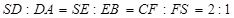 ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )