题目内容
14.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别是F1,F2,离心率是e=$\frac{1}{2}$,P点在椭圆上,△PF1F2的内切圆面积最大值是$\frac{4}{3}$π.(1)求椭圆方程;
(2)若A,B,C,D是椭圆上不重合的四个点,$\overrightarrow{{F}_{1}A}$∥$\overrightarrow{{F}_{1}C}$,$\overrightarrow{{F}_{1}B}$∥$\overrightarrow{{F}_{1}D}$,$\overrightarrow{AC}$•$\overrightarrow{BD}$D=0,求:|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|的范围.
分析 (1)当P为椭圆上、下顶点时,△PF1F2内切圆面积取得最大值,设△PF1F2内切圆半径为r,利用 ${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$|F1F2|•b=bc=$\frac{1}{2}$(|F1F2|+|PF1|+|PF2|)r,化为bc=$\frac{2\sqrt{3}}{3}$(a+c),又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解得a,c,b即可得出;
(2)由题意可得直线AC,BD垂直相交于点F1,由(1)椭圆方程$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1,F1(-2,0).①直线AC,BD有一条斜率不存在时,|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|=14.②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1,y1),C(x2,y2),与椭圆方程联立化为(3+4k2)x2+16k2x+16k2-48=0.利用根与系数的关系可得:|$\overrightarrow{AC}$|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{\frac{24(1+{k}^{2})}{3+4{k}^{2}}}$,把-$\frac{1}{k}$代入上述可得:可得|$\overrightarrow{BD}$|=$\sqrt{\frac{24(1+{k}^{2})}{4+3{k}^{2}}}$,可得|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|=$\sqrt{\frac{168(1+{k}^{2})^{2}}{(4+3{k}^{2})(3+4{k}^{2})}}$,设t=k2+1(k≠0),t>1.即可得出所求范围.
解答 解:(1)设△PF1F2内切圆半径为r,
由△PF1F2的面积为S=$\frac{1}{2}$r(PF1+PF2+F1F2)=$\frac{1}{2}$r(2a+2c),
S最大,则r最大,
当P为椭圆上下顶点时,△PF1F2的面积最大,其内切圆面积取得最大值,
∵$\frac{4}{3}$π=πr2,∴r=$\frac{2\sqrt{3}}{3}$.
${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$|F1F2|•b=bc=$\frac{1}{2}$(|F1F2|+|PF1|+|PF2|)r=$\frac{1}{2}$(2c+2a)×$\frac{2\sqrt{3}}{3}$,
化为bc=$\frac{2\sqrt{3}}{3}$(a+c),
又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解得a=4,c=2,b=2$\sqrt{3}$.
则椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1;
(2)∵$\overrightarrow{{F}_{1}A}$∥$\overrightarrow{{F}_{1}C}$,$\overrightarrow{{F}_{1}B}$∥$\overrightarrow{{F}_{1}D}$,$\overrightarrow{AC}$•$\overrightarrow{BD}$=0,
∴直线AC,BD垂直相交于点F1,
由(1)椭圆方程$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1,F1(-2,0).
①直线AC,BD有一条斜率不存在时,|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|=6+8=14.
②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1,y1),C(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$,化为(3+4k2)x2+16k2x+16k2-48=0.
∴x1+x2=$\frac{-16{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{16{k}^{2}-48}{3+4{k}^{2}}$,
∴|$\overrightarrow{AC}$|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{\frac{24(1+{k}^{2})}{3+4{k}^{2}}}$,
把-$\frac{1}{k}$代入上述可得:可得|$\overrightarrow{BD}$|=$\sqrt{\frac{24(1+{k}^{2})}{4+3{k}^{2}}}$,
∴|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|=$\sqrt{\frac{168(1+{k}^{2})^{2}}{(4+3{k}^{2})(3+4{k}^{2})}}$,
设t=k2+1(k≠0),t>1.
∴|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|=$\sqrt{\frac{168}{12+\frac{t-1}{{t}^{2}}}}$,∵t>1,∴0<$\frac{t-1}{{t}^{2}}$≤$\frac{1}{4}$,
∴|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|∈[$\frac{96}{7}$,14).
综上可得:|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|的取值范围是[$\frac{96}{7}$,14].
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数关系、向量垂直与数量积的关系、三角形内切圆的性质、二次函数的性质,考查了“换元法”、推理能力与计算能力,属于难题.

| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为10销售收入y的值.
参考公式:最小二乘法得$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$其中:$\widehat{b}$是回归方程的斜率,$\widehat{a}$是截距.
| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
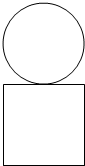 某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )| A. | 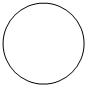 | B. |  | C. | 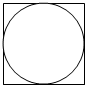 | D. |  |