题目内容
【题目】已知z∈C,z+2i 和 ![]() 都是实数.
都是实数.
(1)求复数z;
(2)若复数(z+ai)2 在复平面上对应的点在第四象限,求实数a 的取值范围.
【答案】
(1)解:设z=a+bi(a,b∈R),则z+2i=a+(b+2)i,
![]() ,
,
∵z+2i 和 ![]() 都是实数,∴
都是实数,∴ 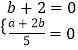 ,解得
,解得 ![]() ,∴z=4﹣2i
,∴z=4﹣2i
(2)解:由(1)知z=4﹣2i,∴(z+ai)2=[4+(a﹣2)i]2=16﹣(a﹣2)2+8(a﹣2)i,
∵(z+ai)2 在复平面上对应的点在第四象限,∴ ![]() ,
,
即 ![]() ,∴
,∴ ![]() ,∴﹣2<a<2,即实数a 的取值范围是(﹣2,2).
,∴﹣2<a<2,即实数a 的取值范围是(﹣2,2).
【解析】(1)化简等式,利用复数为实数的条件求出a,b的值,即得复数z.(2)化简式子,利用复数与复平面内对应点之间的关系列出不等式组,解不等式组求得实数a 的取值范围.
【考点精析】关于本题考查的复数的定义,需要了解形如![]() 的数叫做复数,
的数叫做复数,![]() 和
和![]() 分别叫它的实部和虚部才能得出正确答案.
分别叫它的实部和虚部才能得出正确答案.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目