题目内容
【题目】已知椭圆
（a＞b＞0）的左、右焦点为F1、F2，点A
在椭圆上，且
与x轴垂直．
（1）求椭圆的方程；
（2）过A作直线与椭圆交于另外一点B，求△AOB面积的最大值．
【答案】（1）
；（2）
.
【解析】
试题分析：本题主要考查了椭圆的标准方程和椭圆与直线等基础知识，考查了学生综合运用所学知识，创造性地解决问题的能力、转化能力、计算能力，解题时要认真审题，仔细解答．第一问，由已知：
，
，解得
，
，从而写出方程；第二问，
斜率不存在或斜率存在两种情况讨论，当的斜率存在时，令直线与椭圆方程联立，消参，利用两点间距离公式和点到直线的距离分别求出
和边上的高，代入到三角形面积公式中，计算三角形面积，求出最大值.
试题解析：（1）有已知：，∴，
，
故椭圆方程为
；
（2）当斜率不存在时：
，
当斜率存在时：设其方程为：
，
由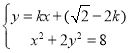
得
，
由已知：
，
即：
，
，
到直线的距离：
，
，
，
，
此时
，
综上所求：当斜率不存在或斜率存在时：
面积取最大值为
．
练习册系列答案
高中必刷题系列答案
相关题目
