题目内容
2.在△ABC中,若A>B,则下列关系中不一定正确的是③.①sinA>sinB②cosA<cosB③sin2A>sin2B④cos2A<cos2B.
分析 ①通过A>B,利用正弦定理,推出sinA>sinB.②由A>B,通过余弦函数的单调性可得cosA<cosB;③由A>B通过举反例说明sin2A>sin2B不正确即可;④由A>B,通过正弦定理以及同角三角函数的基本关系式,以及二倍角的余弦函数推出cos2A<cos2B.
解答 解:由①,∵A>B,则a>b,利用正弦定理可得 a=2rsinA,b=2rsinB,故sinA>sinB.故①正确;
由②,A>B,△ABC中,A、B∈(0,π),余弦函数是减函数,所以cosA<cosB,故②正确;
对于③,例如A=60°,B=45°,满足A>B,但不满足sin2A=$\frac{\sqrt{3}}{2}$,sin2B=1,所以sin2A>sin2B,③不正确;
对于④,因为在△ABC中,A>B,所以a>b,利用正弦定理可得a=2rsinA,b=2rsinB,故sinA>sinB>0,所以
sin2A>sin2B,可得 1-2sin2A<1-2sin2B,由二倍角公式可得:cos2A<cos2B,故④正确.
故答案为:③.
点评 本题考查正弦函数的单调性,正弦定理,同角三角函数的基本关系,三角形中有大角对大边,将命题转化是解题的关键.

练习册系列答案
相关题目
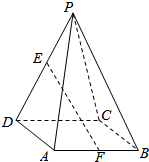 如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,E,F分别为所在边中点,证明:EF∥平面PBC.
如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,E,F分别为所在边中点,证明:EF∥平面PBC.