题目内容
【题目】如图,底面![]() 是边长为3的正方形,
是边长为3的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,又
,又![]() 证出线面垂直
证出线面垂直![]() 平面
平面![]() ,再根据面面垂直的判定定理证出结论;(2) 以
,再根据面面垂直的判定定理证出结论;(2) 以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴建立如图空间直角坐标系
轴建立如图空间直角坐标系![]() ,根据线面角大小求出侧棱长,写出各点坐标,进而求出平面
,根据线面角大小求出侧棱长,写出各点坐标,进而求出平面![]() 和平面
和平面![]() 的法向量,由二面角公式代入求值即可.
的法向量,由二面角公式代入求值即可.
试题解析:(1)![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() .又
.又![]() 底面
底面![]() 是正方形,
是正方形,![]()
![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
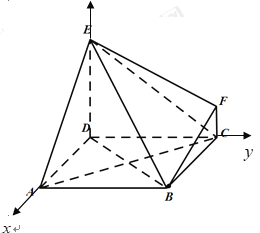
![]() (2)以
(2)以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴建立如图空间直角坐标系
轴建立如图空间直角坐标系![]() ,
,
![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
![]() ,
,![]() .
.![]()
![]() 设平面
设平面![]() 的一个法向量为
的一个法向量为![]() 则
则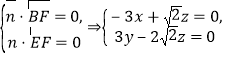 令
令![]() ,则
,则![]() .又
.又![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.![]()
![]() 二面角
二面角![]() 为锐角,
为锐角,![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】如图,在等腰梯形ABCD中,AB=2,CD=4,BC= ![]() ,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得
,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得 ![]() =λ成立,那么实数λ的取值范围为 .
=λ成立,那么实数λ的取值范围为 . 
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占![]() 、家占
、家占![]() 、个人空间占
、个人空间占![]() .如下表:
.如下表:
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |


