题目内容
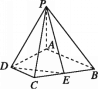
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点. 
(1)求证:PC∥平面BMN;
(2)求证:平面BMN⊥平面PAC. 
【答案】
(1)证明:设AC∩BN=O,连结MO,AN,
因为 ![]() ,N为CD的中点,
,N为CD的中点,
所以AB=CN,AB∥CN,所以四边形ABCN为平行四边形,
所以O为AC的中点,所以MO∥PC.
又因为MO平面BMN,PC平面BMN,所以PC∥平面BMN
(2)证明:(方法一)因为PC⊥平面PDA,AD平面PDA
所以PC⊥AD,由(1)同理可得,四边形ABND为平行四边形,
所以AD∥BN,所以BN⊥PC
因为BC=AB,所以平行四边形ABCN为菱形,所以BN⊥AC,
因为PC∩AC=C,AC平面PAC,PC平面PAC,所以BN⊥平面PAC
因为BN平面BMN,所以平面BMN⊥平面PAC.
(方法二)连结PN,因为PC⊥平面PDA,PA平面PDA,所以PC⊥PA
因为PC∥MO,所以PA⊥MO,因为PC⊥平面PDA,PD平面PDA,所以PC⊥PD
因为N为CD的中点,所以 ![]() ,由(1)
,由(1) ![]() ,所以AN=PN
,所以AN=PN
又因为M为PA的中点,所以PA⊥MN
因为MN∩MO=M,MN平面BMN,MO平面BMN
所以PA⊥平面BMN,因为PA平面PAC,所以平面PAC⊥平面BMN.
【解析】
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目