题目内容
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(
的取值范围.(![]() 是自然对数的底数,
是自然对数的底数,![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)代入a值,求函数的导数,由导数的几何意义求得切线斜率,根据点斜式可得切线方程;(2)求导数,通过讨论a的范围,求函数单调区间,结合函数单调性和函数的最值可求a的范围;(3)求g(x)解析式,求函数导数,讨论函数单调性,由函数单调性和最值可确定a的范围.
(1)当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以切线方程为![]() .
.
(2)![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
因为![]() ,所以
,所以![]() 有唯一零点,即
有唯一零点,即![]() 符合题意;
符合题意;
②当![]() 时,令
时,令![]() ,解得
,解得![]() ,列表如下:
,列表如下:
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
由表可知,![]() .
.
(i)当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 符合题意;
符合题意;
(ii)当![]() ,即
,即![]() 时,
时,![]() ,
,
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
故存在![]() ,使得
,使得![]() ,所以
,所以![]() 不符题意;
不符题意;
(iii)当![]() ,即
,即![]() 时,
时,![]() ,
,
因为![]() ,
,
设![]() ,
,
则![]() ,
,
所以![]() 单调递增,即
单调递增,即![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
故存在![]() ,使得
,使得![]() ,所以
,所以![]() 不符题意;
不符题意;
综上,![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() 符合题意;
符合题意;
②当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
又因为
![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() 不符题意;
不符题意;
综上,![]() 的取值范围为
的取值范围为![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】为了调查某品牌饮料的某种食品添加剂是否超标,现对该品牌下的两种饮料一种是碳酸饮料![]() 含二氧化碳
含二氧化碳![]() ,另一种是果汁饮料
,另一种是果汁饮料![]() 不含二氧化碳
不含二氧化碳![]() 进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶
进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶![]() 均是
均是![]() 组成的一个样本,进行了检测,得到了如下茎叶图
组成的一个样本,进行了检测,得到了如下茎叶图![]() 根据国家食品安全规定当该种添加剂的指标大于
根据国家食品安全规定当该种添加剂的指标大于![]() 毫克
毫克![]() 为偏高,反之即为正常.
为偏高,反之即为正常.
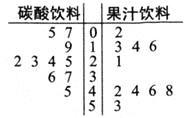
(1)依据上述样本数据,完成下列![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
正常 | 偏高 | 合计 | |
碳酸饮料 | |||
果汁饮料 | |||
合计 |
(2)现从食品添加剂偏高的样本中随机抽取2瓶饮料去做其它检测,求这两种饮料都被抽到的概率.
参考公式: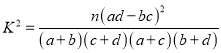 ,其中
,其中![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

