Question

【题目】已知函数f （ x）=ax3+bx2+cx+d 的图象如图所示，则 的取值范围是（ ）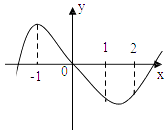
A.（﹣ ， ?）
B.（﹣ ，1）
C.（﹣ ， ）
D.（﹣ ，1）

Answer 1

【答案】D
【解析】解：由图象可知：经过原点，∴f（0）=0=d， ∴f（x）=ax3+bx2+cx．
由图象可得：函数f（x）在[﹣1，1]上单调递减，函数f（x）在x=﹣1处取得极大值．
∴f′（x）=3ax2+2bx+c≤0在[﹣1，1]上恒成立，且f′（﹣1）=0．
得到3a﹣2b+c=0，即c=2b﹣3a，
∵f′（1）=3a+2b+c＜0，
∴4b＜0，即b＜0，
∵f′（2）=12a+4b+c＞0，
∴3a+2b＞0，
设k= ，
建立如图所示的坐标系，则点A（﹣1，﹣1），
则k= 式中变量a、b满足下列条件 ，
作出可行域如图：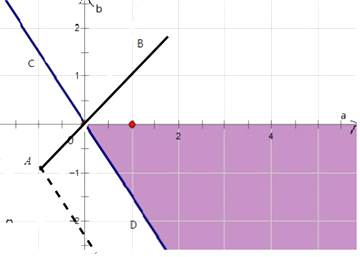

∴k的最大值就是kAO=1，k的最小值就是kCD ，
而kCD就是直线3a+2b=0的斜率，kCD=﹣ ，
∴﹣ ＜k＜1．
故选：D．
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．