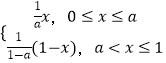题目内容
【题目】已知点P(t,t),点M是圆O1:x2+(y﹣1)2= ![]() 上的动点,点N是圆O2:(x﹣2)2+y2=
上的动点,点N是圆O2:(x﹣2)2+y2= ![]() 上的动点,则|PN|﹣|PM|的最大值是( )
上的动点,则|PN|﹣|PM|的最大值是( )
A.1
B.![]() ﹣2
﹣2
C.2+ ![]()
D.2
【答案】D
【解析】解:如图所示,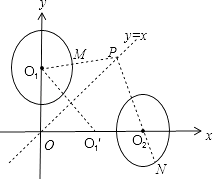
圆O1:x2+(y﹣1)2= ![]() 的圆心O1(0,1),
的圆心O1(0,1),
圆O2:(x﹣2)2+y2= ![]() 的圆心O2(2,0),这两个圆的半径都是
的圆心O2(2,0),这两个圆的半径都是 ![]() ;
;
要使PN﹣PM最大,需PN最大,且PM最小,
由图可得,PN最大值为PO2+ ![]() ,
,
PM的最小值为PO1﹣ ![]() ,
,
故PN﹣PM最大值是(PO2+ ![]() )﹣(PO1﹣
)﹣(PO1﹣ ![]() )=PO2﹣PO1+1,
)=PO2﹣PO1+1,
点P(t,t)在直线 y=x上,O1(0,1)关于y=x的对称点O1′(1,0),
直线O2O1′与y=x的交点为原点O,
则PO2﹣PO1=PO2﹣PO1′≤O1′O2=1,
故PO2﹣PO1+1的最大值为1+1=2,
即|PN|﹣|PM|的最大值为2.
故选D.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目