题目内容
5.若复数z满足2i•z=2+i,则在复平面内,z的共轭复数对应的点坐标是.分析 利用复数代数形式的乘除运算化简求得z,则可求,z的共轭复数对应的点坐标可求.
解答 解:由2i•z=2+i,得,
∴.
∴z的共轭复数对应的点坐标是().
故答案为:.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
13.图1为某村1000户村民月用电量(单位:度)的频率分布直方图,记月用电量在[50,100)的用户数为A1,用电量在[100,150)的用户数为A2,…,以此类推,用电量在[300,350]的用户数为A6,图2是统计图1中村民月用电量在一定范围内的用户数的一个算法流程图.根据图1提供的信息,则图2中输出的s值为( )
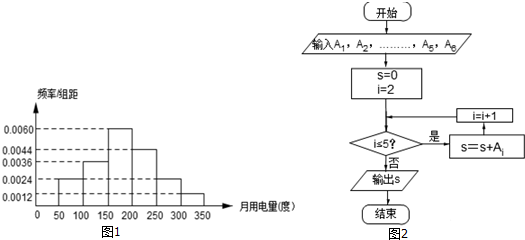

| A. | 820 | B. | 720 | C. | 620 | D. | 520 |
20.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=tanx | B. | y=2x | C. | y=x | D. | y=lg(1+x2) |
17.正弦曲线y=sinx在点(,)的切线方程是( )
| A. | x+2y-+=0 | B. | x-2y+-=0 | C. | x-2y+-π=0 | D. | x+2y-+π=0 |

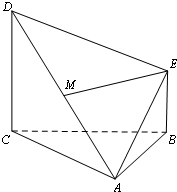 如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=
如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=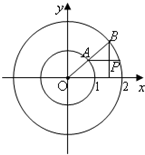 如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=
如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=