题目内容
如图所示,已知椭圆 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A 在椭圆上.
在椭圆上.

(1)求椭圆方程;
(2)点M(x0,y0)在圆x2+y2=b2上,点M在第一象限,过点M作圆x2+y2=b2的切线交椭圆于P、Q两点,问| |+|
|+| |+|
|+| |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由.
 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A 在椭圆上.
在椭圆上.
(1)求椭圆方程;
(2)点M(x0,y0)在圆x2+y2=b2上,点M在第一象限,过点M作圆x2+y2=b2的切线交椭圆于P、Q两点,问|
 |+|
|+| |+|
|+| |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由.(1)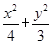 =1(2)4
=1(2)4
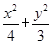 =1(2)4
=1(2)4(1)由右焦点为F2(1,0),可知c=1.设左焦点为F1,则F1(-1,0),又点A 在椭圆上,则
在椭圆上,则
2a=|AF1|+|AF2|=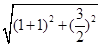 +
+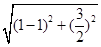 =4,
=4,
∴a=2,b= ,即椭圆方程为
,即椭圆方程为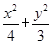 =1;
=1;
(2)设P(x1,y1),Q(x2,y2),则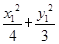 =1(|x1|≤2),
=1(|x1|≤2),
|PF2|2=(x1-1)2+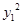 =(x1-1)2+3
=(x1-1)2+3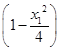 =
=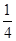 (x1-4)2,
(x1-4)2,
∴|PF2|=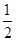 (4-x1)=2-
(4-x1)=2-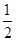 x1.
x1.
连结OM,OP,由相切条件知:
|PM|2=|OP|2-|OM|2=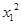 +
+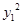 -3=
-3=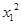 +3
+3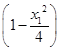 -3=
-3=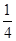
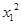 ,
,
显然x1>0,∴|PM|=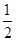 x1.
x1.
∴|PF2|+|PM|=2-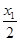 +
+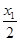 =2.同理|QF2|+|QM|=2-
=2.同理|QF2|+|QM|=2-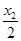 +
+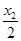 =2.
=2.
∴| |+|
|+| |+|
|+| |=2+2=4为定值.
|=2+2=4为定值.
 在椭圆上,则
在椭圆上,则2a=|AF1|+|AF2|=
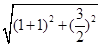 +
+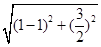 =4,
=4,∴a=2,b=
 ,即椭圆方程为
,即椭圆方程为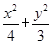 =1;
=1;(2)设P(x1,y1),Q(x2,y2),则
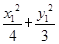 =1(|x1|≤2),
=1(|x1|≤2),|PF2|2=(x1-1)2+
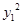 =(x1-1)2+3
=(x1-1)2+3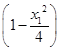 =
=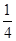 (x1-4)2,
(x1-4)2,∴|PF2|=
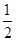 (4-x1)=2-
(4-x1)=2-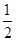 x1.
x1.连结OM,OP,由相切条件知:
|PM|2=|OP|2-|OM|2=
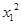 +
+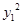 -3=
-3=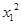 +3
+3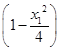 -3=
-3=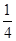
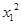 ,
,显然x1>0,∴|PM|=
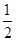 x1.
x1.∴|PF2|+|PM|=2-
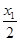 +
+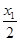 =2.同理|QF2|+|QM|=2-
=2.同理|QF2|+|QM|=2-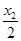 +
+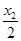 =2.
=2.∴|
 |+|
|+| |+|
|+| |=2+2=4为定值.
|=2+2=4为定值.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
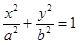 (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线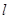 与椭圆C交于不同两点M,N.
与椭圆C交于不同两点M,N. 的长;
的长;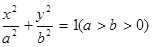 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,点G在椭圆C上,且
,点G在椭圆C上,且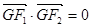 ,
,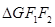 的面积为3.
的面积为3.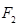 的直线
的直线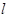 与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于
与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于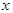 轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由.
轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由.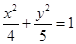 的一个焦点坐标是( )
的一个焦点坐标是( )

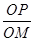 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.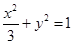 的焦距为( )
的焦距为( )
 +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率. =2
=2 ,求直线AB的方程.
,求直线AB的方程. 的左右焦点为
的左右焦点为 ,若存在动点
,若存在动点 ,满足
,满足 ,且
,且 的面积等于
的面积等于 ,则椭圆离心率的取值范围是 .
,则椭圆离心率的取值范围是 .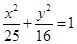 上的一点
上的一点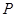 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为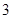 ,则
,则