题目内容
已知椭圆C: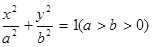 的离心率为
的离心率为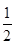 ,左、右焦点分别为
,左、右焦点分别为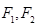 ,点G在椭圆C上,且
,点G在椭圆C上,且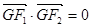 ,
,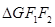 的面积为3.
的面积为3.
(1)求椭圆C的方程:
(2)设椭圆的左、右顶点为A,B,过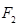 的直线
的直线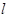 与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于
与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于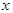 轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由.
轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由.
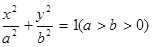 的离心率为
的离心率为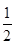 ,左、右焦点分别为
,左、右焦点分别为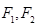 ,点G在椭圆C上,且
,点G在椭圆C上,且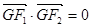 ,
,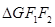 的面积为3.
的面积为3.(1)求椭圆C的方程:
(2)设椭圆的左、右顶点为A,B,过
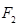 的直线
的直线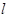 与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于
与椭圆交于不同的两点M,N(不同于点A,B),探索直线AM,BN的交点能否在一条垂直于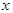 轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由.
轴的定直线上,若能,求出这条定直线的方程;若不能,请说明理由.(1) ;(2)直线AM,BN的交点必在一条垂直于
;(2)直线AM,BN的交点必在一条垂直于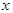 轴的定直线上,这条直线的方程是
轴的定直线上,这条直线的方程是 .
.
 ;(2)直线AM,BN的交点必在一条垂直于
;(2)直线AM,BN的交点必在一条垂直于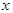 轴的定直线上,这条直线的方程是
轴的定直线上,这条直线的方程是 .
.试题分析:(1)求椭圆
 的方程,由椭圆
的方程,由椭圆 的离心率为
的离心率为 ,得
,得 ,
,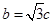 ,由
,由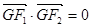 得,
得, ,得得
,得得 ,即
,即 ,由
,由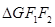 的面积为3,得
的面积为3,得 ,由于
,由于 ,可得
,可得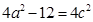 ,即
,即 ,可求出
,可求出 ,从而可得
,从而可得 ,即得椭圆
,即得椭圆 的方程;(2)这是探索性命题,由于探索直线AM,BN的交点能否在一条垂直于
的方程;(2)这是探索性命题,由于探索直线AM,BN的交点能否在一条垂直于 轴的定直线上,可有特例求出定直线,然后验证一般情况,故当直线
轴的定直线上,可有特例求出定直线,然后验证一般情况,故当直线 的斜率不存在时,直线
的斜率不存在时,直线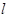 :
: ,直线
,直线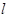 与椭圆C的交点坐标
与椭圆C的交点坐标 ,
, ,写出直线
,写出直线 的方程,解交点坐标为
的方程,解交点坐标为 ,它在垂直于
,它在垂直于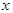 轴的直线
轴的直线 上,然后验证当直线
上,然后验证当直线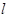 的斜率存在时,交点必在直线
的斜率存在时,交点必在直线 上即可,因此设直线
上即可,因此设直线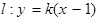 ,代入椭圆C的方程
,代入椭圆C的方程 ,设
,设 ,利用根与系数关系,得关系式,再写出直线
,利用根与系数关系,得关系式,再写出直线 的方程,消去
的方程,消去 ,解方程得
,解方程得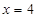 即可.
即可.试题解析:(1)设
 ,由于
,由于 ,所以
,所以 ,
,根据
 ,得
,得 ,即
,即 ,
,因为
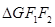 的面积为3,
的面积为3,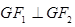 ,所以
,所以 ,
,所以有
 ,解得
,解得 ,所以
,所以 ,
,所以椭圆才C的方程为
 。 5分
。 5分(2)由(1)知
 。
。①当直线
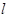 的斜率不存在时,直线
的斜率不存在时,直线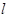 :
: ,直线
,直线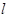 与椭圆C的交点坐标
与椭圆C的交点坐标 ,
, ,此时直线
,此时直线 ,联立两直线方程,解得两直线的交点坐标(4,3)。它在垂直于
,联立两直线方程,解得两直线的交点坐标(4,3)。它在垂直于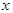 轴的直线
轴的直线 上。 7分
上。 7分②当直线
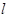 的斜率存在时,
的斜率存在时,设直线
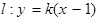 ,代入椭圆C的方程
,代入椭圆C的方程 ,整理得
,整理得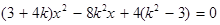 ,设直线
,设直线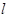 与椭圆C的交点
与椭圆C的交点 ,则
,则 。
。直线AM的方程为
 ,即
,即 ,
,直线BN的方程为
 ,即
,即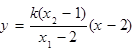
由直线AM与直线BN的方程消去
 ,得
,得

所以直线AM与直线BN的交点在直线
 上。 12分
上。 12分综上所述,直线AM,BN的交点必在一条垂直于
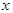 轴的定直线上,这条直线的方程是
轴的定直线上,这条直线的方程是 . 13分
. 13分
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点. (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线 与椭圆C交于不同两点
与椭圆C交于不同两点 .
. 的长;
的长; 轴于点P(0,y0),求
轴于点P(0,y0),求 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
 的焦点为焦点,且过
的焦点为焦点,且过 点的双曲线的标准方程.
点的双曲线的标准方程. 在椭圆+=1上,若A点的坐标为(3,0),
在椭圆+=1上,若A点的坐标为(3,0), ,且
,且 ,则
,则 的最小值为________。
的最小值为________。 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A 在椭圆上.
在椭圆上.
 |+|
|+| |+|
|+| |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由. =1上的一点,F1,F2分别是该椭圆的左、右焦点,若|PF1|∶|PF2|=2∶1,则△PF1F2的面积为( ).
=1上的一点,F1,F2分别是该椭圆的左、右焦点,若|PF1|∶|PF2|=2∶1,则△PF1F2的面积为( ).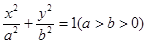 的左、右顶点分别为
的左、右顶点分别为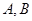 ,左、右焦点分别为
,左、右焦点分别为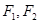 ,若
,若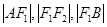 成等比数列,则此椭圆的离心率为( )
成等比数列,则此椭圆的离心率为( )


