题目内容
（本小题满分13分）用一块长为a，宽为b (a＞b)的矩形木块，在二面角为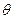
(0＜＜
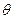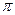)的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面，两边与墙面贴紧，另一边与地面贴紧)，试问怎样围才能使储物仓的容积最大？并求出这个最大值．
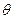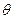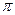(0＜＜)的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面，两边与墙面贴紧，另一边与地面贴紧)，试问怎样围才能使储物仓的容积最大？并求出这个最大值．最大值为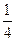
a2b cot
．
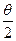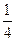a2b cot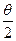．（1）若使矩形木板长边贴紧地面，即AB =" CD" = a，AD =" BC" = b，设PA = x，PB = y，则a2 = x2 + y2 – 2xy cos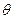≥2xy – 2xy cos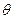．∴xy≤
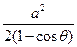(当且仅当x = y时取等号) ．…5分
这时容积V1 = (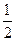
xy sin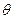)·b≤
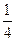= a2b cot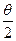．……8分
（2）若使矩形木板短边贴紧地面，则同理可得xy ≤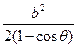
．这时容积V2 = (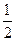xy sin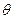)·a ≤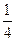ab2 cot 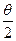∵a＞b＞0，cot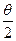＞0 ∴V1＞V2．……12分
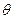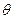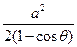≥2xy – 2xy cos．∴xy≤ (当且仅当x = y时取等号) ．…5分这时容积V1 = (
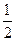xy sin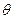)·b≤ = 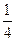a2b cot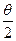．……8分（2）若使矩形木板短边贴紧地面，则同理可得xy ≤
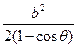．这时容积V2 = (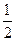xy sin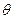)·a ≤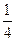ab2 cot 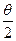∵a＞b＞0，cot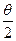＞0 ∴V1＞V2．……12分
练习册系列答案
相关题目
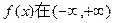上满足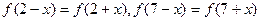
，且在闭区间[0，7]上，只有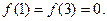
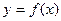的奇偶性；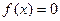
在闭区间[－2005，2005]上的根的个数，并证明你的结论．
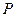在正方体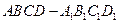
的对角线
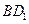上．过点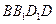
的直线，与正方体表面相交于
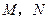．设
，
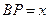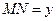，则函数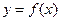
的图象大致是（ ）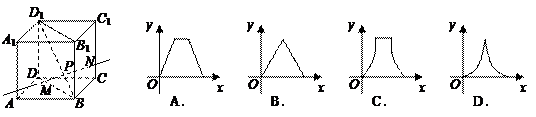
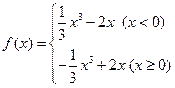,下列四个命题中：①
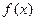是奇函数; ②
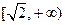上是减函数.其中说法正确的命题序号是 . (写出所有正确命题的序号).
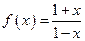，又记
（ ）
；
；
；
；
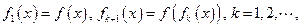
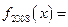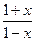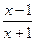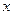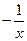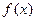的定义域为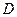
，如果对于任意的
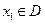，存在唯一的
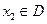，使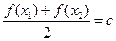
（
为常数）成立，则称函数
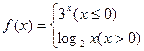，那么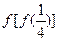
的值为 ( ) 
