题目内容
16．比较大小：（1）1.3${\;}^{\frac{1}{2}}$＜1.5${\;}^{\frac{1}{2}}$；（2）5.1-2＜5.09-2．分析 （1）利用函数f（x）=$\sqrt{x}$在（0，+∞）上单调递增，即可得出；
（2）利用函数f（x）=x-2在（0，+∞）上单调递减，即可得出．
解答 解：（1）由于函数f（x）=$\sqrt{x}$在（0，+∞）上单调递增，1.3＜1.5，
∴1.3${\;}^{\frac{1}{2}}$＜1.5${\;}^{\frac{1}{2}}$；
（2）由于函数f（x）=x-2在（0，+∞）上单调递减，5.1＞5.09，
∴5.1-2＜5.09-2．
故答案分别为：＜；＜．
点评 本题考查了幂函数的单调性，考查了推理能力与计算能力，属于基础题．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
1．已知log2[log3（log4x）]=0，那么x等于（ ）
| A． | 1 | B． | 16 | C． | 64 | D． | 81 |
4．
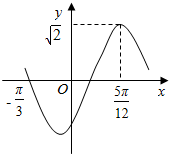函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）
函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）| A． | $[\frac{5π}{12}+kπ，\frac{11π}{12}+kπ]，k∈z$ | B． | $[\frac{5π}{6}+kπ≤x≤\frac{11π}{6}+kπ]，k∈z$ | ||
| C． | $[\frac{5π}{12}+2kπ，\frac{11π}{12}+2kπ]，k∈z$ | D． | $[-\frac{π}{12}+kπ，\frac{5π}{12}+kπ]，k∈z$ |