题目内容
19．若曲线y=xlnx在点（e，e）处的切线与直线x+ay=1垂直，则实数a=2．分析 利用导数求出曲线y=xlnx在点（e，e）处的切线斜率，根据切线与直线x+ay=1垂直的关系，求出a的值．
解答 解：∵y=xlnx，x＞0；
∴y′=lnx+1，
当x=e时，y′=lne+1=2；
∴曲线y=xlnx在点（e，e）处的切线斜率为k=2，
又该切线与直线x+ay=1垂直，
∴-$\frac{1}{a}$•2=-1，
解得a=2．
故答案为：2．
点评 本题考查了利用导数求曲线的切线方程的斜率问题，也考查了直线方程的垂直与应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
9．已知集合A={x|-1≤x≤1}，B={x|x2-5x+6≥0}，则下列结论中正确的是（ ）
| A． | A∩B=B | B． | A∪B=A | C． | A?B | D． | ∁RA=B |
10．设Sn为等比数列{an}的前n项和，若8a3+a6=0，则$\frac{{S}_{6}}{{S}_{2}}$=（ ）
| A． | -11 | B． | -21 | C． | 11 | D． | 21 |
7．
在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$，$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$，$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是（ ）
在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$，$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$，$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是（ ）| A． | -$\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | B． | -$\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | C． | $\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | D． | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ |
14．若抛物线y2=2px的焦点与双曲线$\frac{{x}^{2}}{3}$-y2=1的右焦点重合，则p=（ ）
| A． | $\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 2 | D． | 4 |
11．设α=2014°，则下列判断正确的是（ ）
| A． | sinα＞0，cosα＞0，tanα＞0 | B． | sinα＞0，cosα＜0，tanα＜0 | ||
| C． | sinα＜0，cosα＜0，tanα＞0 | D． | sinα＜0，cosα＞0，tanα＜0 |
8．若将如图的展开图还原成成正方体，则∠ABC的度数为（ ）
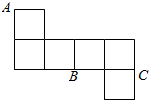
| A． | 120° | B． | 90° | C． | 60° | D． | 45° |