题目内容
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 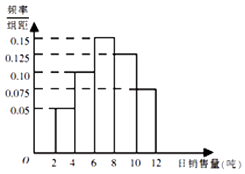
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用X表示未来3天内日销售量不低于8吨的天数,求随机变量X的分布列及数学期望.
【答案】
(1)解:由频率分布直方图可知,
日销售量不低于8吨的频率为:2×(0.125+0.075)=0.4,
记未来3天内,第i天日销售量不低于8吨为事件A1(i=1,2,3),
则P(A1)=0.4,
未来3天内,连续2天日销售不低于8吨,
另一天日销量低于8吨包含两个互斥事件 ![]() 和
和 ![]() ,
,
则未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率:
![]()
=0.4×0.4×(1﹣0.4)+(1﹣0.4)×0.4×0.4=0.192
(2)解:X的可能取值为0,1,2,3,且X~B(3,0.4)
P(X=0)=(1﹣0.4)3=0.216,
![]() ,
,
![]() ,
,
P(X=3)=0.43=0.064,
∴X的分布列为:
X | 0 | 1 | 2 | 3 |
P | 0.216 | 0.432 | 0.288 | 0.064 |
E(X)=3×0.4=1.2
【解析】(Ⅰ)由频率分布直方图求出日销售量不低于8吨的频率为0.4,记未来3天内,第i天日销售量不低于8吨为事件A1(i=1,2,3),未来3天内,连续2天日销售不低于8吨,另一天日销量低于8吨包含两个互斥事件 ![]() 和
和 ![]() ,由此能求出未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率.(Ⅱ)X的可能取值为0,1,2,3,且X~B(3,0.4),由此能求出X的分布列和E(X).
,由此能求出未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率.(Ⅱ)X的可能取值为0,1,2,3,且X~B(3,0.4),由此能求出X的分布列和E(X).

【题目】某校书法兴趣组有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加书法比赛![]() 每人被选到的可能性相同
每人被选到的可能性相同![]() .
.
![]() 用表中字母列举出所有可能的结果;
用表中字母列举出所有可能的结果;
![]() 设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.