题目内容
【题目】已知矩形ABCD的长AB=4,宽AD=3,将其沿对角线BD折起,得到四面体A﹣BCD,如图所示,给出下列结论:
①四面体A﹣BCD体积的最大值为 ![]() ;
;
②四面体A﹣BCD外接球的表面积恒为定值;
③若E、F分别为棱AC、BD的中点,则恒有EF⊥AC且EF⊥BD;
④当二面角A﹣BD﹣C为直二面角时,直线AB、CD所成角的余弦值为 ![]() ;
;
⑤当二面角A﹣BD﹣C的大小为60°时,棱AC的长为 ![]() .
.
其中正确的结论有(请写出所有正确结论的序号).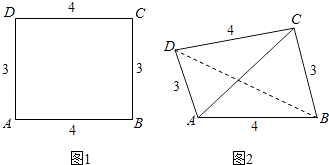
【答案】②③④
【解析】解:①四面体ABCD体积最大值为两个面互相垂直,四面体A﹣BCD体积的最大值为 ![]() =
= ![]() ,故不正确;
,故不正确;
②三棱锥A﹣BCD外接球的半径为 ![]() ,所以三棱锥A﹣BCD外接球的表面积为4
,所以三棱锥A﹣BCD外接球的表面积为4 ![]() =25π;②正确;
=25π;②正确;
③若E、F分别为棱AC、BD的中点,连接AF,CF则AF=CF,根据等腰三角形三线合一得到EF⊥AC;
连接DE,BE,容易判断△ACD≌△ACB,得到DE=BE,所以EF⊥BD;所以③正确;
④当二面角A﹣BD﹣C为直二面角时,以C为原点CB,CD所在直线分别为x,y轴,则由向量的数量积可以得到直线AB、CD所成角的余弦值为 ![]() ,所以④正确.
,所以④正确.
⑤当二面角A﹣BD﹣C的大小为60°时,棱AC的长为 ![]() ,在直角三角形ABD中,AB=4,AD=3,BD=5,
,在直角三角形ABD中,AB=4,AD=3,BD=5,
作AE⊥BD,CF⊥BD,则AE=CF= ![]() ,DE=BF=
,DE=BF= ![]() ,
,
同理直角三角形ABC中,则EF=BD﹣DE﹣BF= ![]() ,
,
在平面ABD内,过F作FH∥AE,且FH=AE,连接AH,易得四边形AEFH为矩形,
则AH=EF= ![]() ,AH∥EF,
,AH∥EF,
FH⊥DB,又CF⊥DB,即有∠CFH为二面角C﹣BD﹣A的平面角,且为60°,
即CH=CF= ![]() ,
,
由BD⊥平面CFH,得到BD⊥CH,即有AH⊥CH,
则AC= ![]() =
= ![]() ,故⑤错误;
,故⑤错误;
所以答案是:②③④.
【考点精析】本题主要考查了棱锥的结构特征的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方才能正确解答此题.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案