Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕļ£į∂ŌŖ![]() “Ľ≤ŗ
“Ľ≤ŗ![]() ī¶”–“ĽłŲ√ņņŲĶń–°Ķļ£¨ń≥¬√”őĻęňĺő™∑ĹĪ„”őŅÕ£¨‘ŕ
ī¶”–“ĽłŲ√ņņŲĶń–°Ķļ£¨ń≥¬√”őĻęňĺő™∑ĹĪ„”őŅÕ£¨‘ŕ![]() …Ō…ŤŃĘŃň
…Ō…ŤŃĘŃň![]() ŃĹłŲĪ®√ŻĶ„£¨¬ķ◊„
ŃĹłŲĪ®√ŻĶ„£¨¬ķ◊„![]() ÷–»ő“‚ŃĹĶ„ľšĶńĺŗņŽő™
÷–»ő“‚ŃĹĶ„ľšĶńĺŗņŽő™![]() .Ļęňĺń‚įī“‘Ō¬ňľ¬∑‘ň◊ų£ļŌ»Ĺę
.Ļęňĺń‚įī“‘Ō¬ňľ¬∑‘ň◊ų£ļŌ»Ĺę![]() ŃĹī¶”őŅÕ∑÷Īū≥ň≥ĶľĮ÷–ĶĹ
ŃĹī¶”őŅÕ∑÷Īū≥ň≥ĶľĮ÷–ĶĹ![]() ÷ģľšĶń÷–◊™Ķ„
÷ģľšĶń÷–◊™Ķ„![]() ī¶(Ķ„
ī¶(Ķ„![]() “ž”ŕ
“ž”ŕ![]() ŃĹĶ„)£¨»Ľļů≥ňÕ¨“Ľň“¬÷”ő¬÷«įÕý
ŃĹĶ„)£¨»Ľļů≥ňÕ¨“Ľň“¬÷”ő¬÷«įÕý![]() Ķļ£ģĺ›Õ≥ľ∆£¨√ŅŇķ”őŅÕ
Ķļ£ģĺ›Õ≥ľ∆£¨√ŅŇķ”őŅÕ![]() ī¶–Ť∑Ę≥Ķ2Ńĺ£¨
ī¶–Ť∑Ę≥Ķ2Ńĺ£¨ ![]() ī¶–Ť∑Ę≥Ķ4Ńĺ£¨√ŅŃĺ∆Ż≥Ķ√Ņ«ß√◊ļń∑—
ī¶–Ť∑Ę≥Ķ4Ńĺ£¨√ŅŃĺ∆Ż≥Ķ√Ņ«ß√◊ļń∑—![]() ‘™£¨”ő¬÷√Ņ«ß√◊ļń∑—
‘™£¨”ő¬÷√Ņ«ß√◊ļń∑—![]() ‘™£ģ£®∆š÷–
‘™£ģ£®∆š÷–![]() «’ż≥£ ż£©…Ť°Ō
«’ż≥£ ż£©…Ť°Ō![]() £¨√ŅŇķ”őŅÕī”łų◊‘Ī®√ŻĶ„ĶĹ
£¨√ŅŇķ”őŅÕī”łų◊‘Ī®√ŻĶ„ĶĹ![]() Ķļňý–Ť‘ň š≥…Īĺő™
Ķļňý–Ť‘ň š≥…Īĺő™![]() ‘™£ģ
‘™£ģ
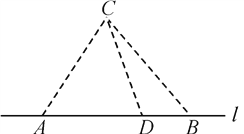
(1) –ī≥Ų![]() Ļō”ŕ
Ļō”ŕ![]() ĶńļĮ żĪŪīÔ Ĺ£¨≤Ę÷ł≥Ų
ĶńļĮ żĪŪīÔ Ĺ£¨≤Ę÷ł≥Ų![]() Ķń»°÷Ķ∑∂őߣĽ
Ķń»°÷Ķ∑∂őߣĽ
(2) ő £ļ÷–◊™Ķ„![]() ĺŗņŽ
ĺŗņŽ![]() ī¶∂ŗ‘∂ Ī£¨
ī¶∂ŗ‘∂ Ī£¨ ![]() ◊Ó–°£Ņ
◊Ó–°£Ņ
°ĺīūįł°Ņ(1) ![]() £Ľ£®2£©
£Ľ£®2£©![]() .
.
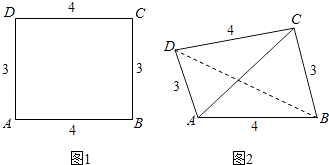
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©‘ŕ![]() ÷–£¨«ů≥ŲŌŗĻōĶńĹ«£¨ņŻ”√’żŌ“∂®ņŪ£¨«ů≥Ų
÷–£¨«ů≥ŲŌŗĻōĶńĹ«£¨ņŻ”√’żŌ“∂®ņŪ£¨«ů≥Ų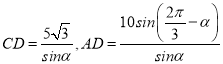 £¨ĪŪ ĺ≥Ųňý–Ť‘ň š≥…Īĺő™
£¨ĪŪ ĺ≥Ųňý–Ť‘ň š≥…Īĺő™![]() ‘™Ļō”ŕ
‘™Ļō”ŕ![]() ĶńļĮ żĪŪīÔ Ĺ£Ľ£®2£©ņŻ”√ļĮ żĪŪīÔ Ĺ£¨«ů≥ŲļĮ żĶńĶľ ż£¨Õ®ĻżĶľ żĶń∑ŻļŇ£¨Ň–∂ŌĶ•Ķų–‘«ůĹ‚ļĮ żĶń◊Ó÷Ķ.
ĶńļĮ żĪŪīÔ Ĺ£Ľ£®2£©ņŻ”√ļĮ żĪŪīÔ Ĺ£¨«ů≥ŲļĮ żĶńĶľ ż£¨Õ®ĻżĶľ żĶń∑ŻļŇ£¨Ň–∂ŌĶ•Ķų–‘«ůĹ‚ļĮ żĶń◊Ó÷Ķ.
‘Ő‚Ĺ‚őŲ£ļ(1) ”…Ő‚÷™‘ŕ°ųACD÷–£¨°ŌCAD£Ĺ![]() £¨°ŌCDA£Ĺ¶Ń£¨AC£Ĺ10£¨°ŌACD£Ĺ
£¨°ŌCDA£Ĺ¶Ń£¨AC£Ĺ10£¨°ŌACD£Ĺ![]() £≠¶Ń.
£≠¶Ń.
”…’żŌ“∂®ņŪ÷™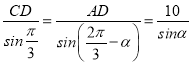 £¨
£¨
ľīCD£Ĺ![]() £¨ AD£Ĺ
£¨ AD£Ĺ £¨
£¨
ňý“‘S£Ĺ4aAD£ę8aBD£ę12aCD£Ĺ (12CD£≠4AD£ę80)a
£Ĺ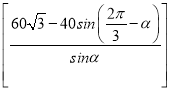 a£ę80a £Ĺ
a£ę80a £Ĺ![]() a£ę60a
a£ę60a![]()
(2) S°š£Ĺ20 ![]() £¨
£¨
ŃÓS°š£Ĺ0Ķ√cos ¶Ń£Ĺ![]()
ĶĪcos ¶Ń>![]() Ī£¨S°š<0£Ľ ĶĪcos ¶Ń
Ī£¨S°š<0£Ľ ĶĪcos ¶Ń![]() < Ī£¨S°š>0£¨
< Ī£¨S°š>0£¨
ňý“‘ĶĪcos ¶Ń£Ĺ![]() Ī£¨S»°Ķ√◊Ó–°÷Ķ£¨
Ī£¨S»°Ķ√◊Ó–°÷Ķ£¨
īň Īsin ¶Ń£Ĺ![]() £¨AD£Ĺ
£¨AD£Ĺ![]() £Ĺ5£ę
£Ĺ5£ę![]() £¨
£¨
ňý“‘÷–◊™Ķ„CĺŗAī¶![]() km Ī£¨‘ň š≥…ĪĺS◊Ó–°£ģ
km Ī£¨‘ň š≥…ĪĺS◊Ó–°£ģ

 √Ż ¶÷łĶľ∆ŕń©≥ŚīŐĺŪŌĶŃ–īūįł
√Ż ¶÷łĶľ∆ŕń©≥ŚīŐĺŪŌĶŃ–īūįł Ņ™–ńÕ‹Ņŕň„Ő‚Ņ®ŌĶŃ–īūįł
Ņ™–ńÕ‹Ņŕň„Ő‚Ņ®ŌĶŃ–īūįł