题目内容
15.等差数列{an}中,a2=4,a4+a7=15.(1)求数列{an}的通项公式;
(2)设bn=2an-2+n,求{bn}的前n项和Sn.
(3)求数列{$\frac{1}{{{a}_{n}}^{2}-1}$}的前n项和Tn.
分析 (1)利用等差数列的通项公式即可得出;
(2)利用等差数列与等比数列的前n项和公式即可得出;
(3)利用“裂项求和”即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a2=4,a4+a7=15.
∴$\left\{\begin{array}{l}{{a}_{1}+d=4}\\{2{a}_{1}+9d=15}\end{array}\right.$,解得a1=3,d=1.
∴an=3+(n-1)=n+2.
(2)bn=2an-2+n=2n+n,
∴{bn}的前n项和Sn=$\frac{2({2}^{n}-1)}{2-1}$+$\frac{n(n+1)}{2}$=2n+1-2+$\frac{n(n+1)}{2}$.
(3)$\frac{1}{{{a}_{n}}^{2}-1}$=$\frac{1}{(n+2)^{2}-1}$=$\frac{1}{(n+1)(n+3)}$=$\frac{1}{2}(\frac{1}{n+1}-\frac{1}{n+3})$.
∴前n项和Tn=$\frac{1}{2}[(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})$+$(\frac{1}{4}-\frac{1}{6})$+…+$(\frac{1}{n}-\frac{1}{n+2})+(\frac{1}{n+1}-\frac{1}{n+3})]$
=$\frac{1}{2}(\frac{1}{2}+\frac{1}{3}-\frac{1}{n+2}-\frac{1}{n+3})$
=$\frac{5}{12}$-$\frac{2n+5}{2(n+2)(n+3)}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

| A. | (-∞,-3) | B. | (4,+∞) | C. | (-∞,1) | D. | (-∞,-4) |
| A. | ($\frac{4}{3}$,$\frac{4}{3}$,$\frac{4}{3}$) | B. | ($\frac{8}{3}$,$\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\frac{4}{3}$,$\frac{8}{3}$) | D. | ($\frac{8}{3}$,$\frac{8}{3}$,$\frac{4}{3}$) |
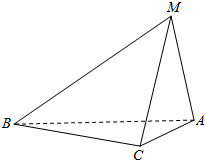 如图,在直角三角形BMC中,∠BCM=90°,∠MBC=60°,BM=5,MA=3,且MA⊥AC,AB=4.求MC与平面ABC所成角的正弦值.
如图,在直角三角形BMC中,∠BCM=90°,∠MBC=60°,BM=5,MA=3,且MA⊥AC,AB=4.求MC与平面ABC所成角的正弦值.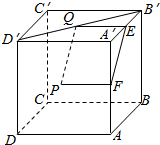 已知正方体ABCD-A′B′C′D′的棱长为a,点P是平面AA′D′D的中心,Q为B′D′上一点,且PQ∥平面AA′B′B,求线段PQ的长.
已知正方体ABCD-A′B′C′D′的棱长为a,点P是平面AA′D′D的中心,Q为B′D′上一点,且PQ∥平面AA′B′B,求线段PQ的长.