题目内容
3．在等比数列{an}中，a2=18，a4=8，则a1=27或-27，q=$\frac{2}{3}$或-$\frac{2}{3}$．分析 由已知条件利用等比数列的通项公式列出方程组，由此能求出等比数列的首项和公比．
解答 解：∵在等比数列{an}中，a2=18，a4=8，
∴$\left\{\begin{array}{l}{{a}_{1}q=18}\\{{a}_{1}{q}^{3}=8}\end{array}\right.$，
解得a1=27，q=$\frac{2}{3}$，或a1=-27，q=-$\frac{2}{3}$．
故答案为：27或-27，$\frac{2}{3}$或-$\frac{2}{3}$．
点评 本题考查等比数列的首项和公比的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
相关题目
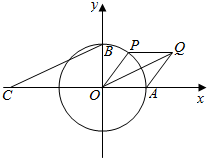如图所示，A，B分别是单位圆与x轴、y轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），C点坐标为（-2，0），四边形OAQP是平行四边形．
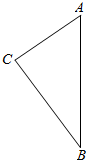已知等腰三角形ABC中CA=CB，底边长AB=2，现以边AB为轴旋转一周，得旋转体．
正方体中，E，F，G分别是A′D′、B′C′、D′C′的中点．