Question

【题目】设是实数，已知奇函数,

（1）求的值；

（2）证明函数在R上是增函数;

（3）若对任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0有解，求k的取值范围．

Answer 1

【答案】（1）1；（2）见解析；（3）

【解析】

(1)由奇函数的性质可得，可解得的值,验证即可得结论；(2)由（1）的结论，可得，在已知区间上任取；作差、变形和定符号、由作差法分析可得结论；(3)根据题意,由函数的奇偶性与单调性分析，原不等式可以变形为，进而可得，求得的最小值，即可得结果.

（1）∵f（x）为R奇函数，∴f（0）=0，，

解得a=1

（2）由（1）的结论，，

设，则，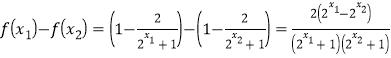

又由，，

则，

则函数在是增函数.

（3）∵f（x）为奇函数，由不等式f（t2﹣2t）+f（2t2﹣k）＜0化为

f（t2﹣2t）＜﹣f（2t2﹣k），即f（t2﹣2t）＜f（k﹣2t2），

又∵f（t）为增函数，t2﹣2t＜k﹣2t2，∴3t2﹣2t＜k．

当t=﹣时，3t2﹣2t有最小值﹣，∴k>-.