题目内容
【题目】已知函数![]() ,
, ![]() .
.
(![]() )若
)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(![]() )若
)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
(![]() )若
)若![]() ,且
,且![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() (3)
(3) ![]()
【解析】试题分析:
(1)求出导函数![]() ,切线方程为
,切线方程为![]() ,化简即得;
,化简即得;
(2)求出导函数![]() ,由不等式
,由不等式![]() 得增区间,由不等式
得增区间,由不等式![]() 得减区间;
得减区间;
(3)题意说明![]() ,因此求出导函数
,因此求出导函数![]() ,
, ![]() 的零点有
的零点有![]() 和1,因此按
和1,因此按![]() 与
与![]() 的大小进行分类讨论,求得
的大小进行分类讨论,求得![]() 的最小值,然后由
的最小值,然后由![]() 可得.
可得.
试题解析:
(![]() )
)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
∴切线方程为![]() .
.
(![]() )
)![]() ,
, ![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(3)![]() 时,
时, ![]() 在区间
在区间![]() 恒成立,即
恒成立,即![]() ,
,
![]() ,
,
令![]() 则
则![]() ,
, ![]() .
.
①![]() 即
即![]() 时,
时, ![]() ,
, ![]() 在
在![]() ,
,
![]() 恒成立.
恒成立.
②![]() 时,即
时,即![]() ,
,
![]() 在
在![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() .
.
③![]() 时,即
时,即![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
∴![]() ,
,
即![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() .
.
④![]() ,即
,即![]() ,
,
![]() ,
,
∴![]() 即
即![]() 不符合.
不符合.
⑤![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,即
,即![]() 不符合,
不符合,
综上: ![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了很大的便利,但也给城市的管理带来了一些困难,现某城市为了解人们对“共享单车”投放的认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 赞成投放的人数 | 赞成投放的人数占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|
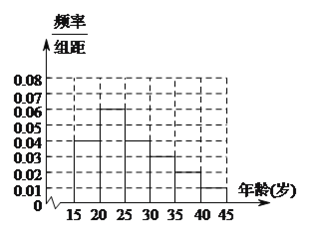
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取
)在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取![]() 人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
(![]() )在(
)在(![]() )中抽取的
)中抽取的![]() 人中随机选派
人中随机选派![]() 人作为领队,求所选派的
人作为领队,求所选派的![]() 人中第五组至少有一人的概率.
人中第五组至少有一人的概率.