题目内容
【题目】已知f（x）是R上的奇函数，且x>0时，f（x）=x2-4x+3．
求：（1）f（x）的解析式．
（2）已知t＞0，求函数f（x）在区间[t，t+1]上的最小值．
【答案】（1）f（x）=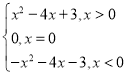
（2）
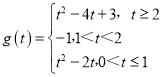
【解析】
（1）当x＜0时，-x＞0，而f（x）=-f（-x）可求f（x）
（2）由题意可得函数f（x）[t，t+1]上f（x）=x2-4x+3=（x-2）2-1开口向上且关于x=2对称
①当t+1≤2时，函数f（x）在[t，t+1]上单调递减，g（t）=f（t+1）
②当t＜2＜t+1时即1＜t＜2时，对称轴在区间内，g（t）=f（2）
③当t≥2时，函数f（x）在[t，t+1]上单调递增，g（t）=f（t）
（1）∵f（x）是奇函数
∴f（-x）=-f（x）对任意的x都成立, f（0）=0
又x>0时，f（x）=x2-4x+3．
∴x＜0时，-x＞0
∴f（x）=-f（-x）=-[（-x）2-4（-x）+3]=-x2-4x-3
∴f（x）=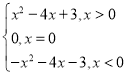
（2）∵t＞0
∴当x∈[t，t+1]时，f（x）=x2-4x+3=（x-2）2-1开口向上且关于x=2对称
①当t+1≤2时，函数f（x）在[t，t+1]上单调递减
∴g（t）=f（t+1）=（t-1）2-1=t2-2t
②当t＜2＜t+1时即1＜t＜2时，对称轴在区间内
∴g（t）=f（2）=-1
③当t≥2时，函数f（x）在[t，t+1]上单调递增
∴g（t）=f（t）=t2-4t+3
综上所述，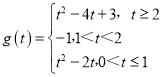
【题目】根据以往的经验，某建筑工程施工期间的降水量
（单位：
）对工期的影响如下表：
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料，某调查小组抄录了该工程施工地某月前
天的降水量的数据，绘制得到降水量的折线图，如下图所示.
（1）求这天的平均降水量；
（2）根据降水量的折线图，分别估计该工程施工延误天数
的概率.
