题目内容
在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则
=
,推广到空间可以得到类似结论;已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
=______.
| S1 |
| S2 |
| 1 |
| 4 |
| V1 |
| V2 |
从平面图形类比空间图形,从二维类比三维,
可得如下结论:正四面体的外接球和内切球的半径之比是 3:1
故正四面体P-ABC的内切球体积为V1,外接球体积为V2之比等于
=(
)3=
.
故答案为:
.

可得如下结论:正四面体的外接球和内切球的半径之比是 3:1
故正四面体P-ABC的内切球体积为V1,外接球体积为V2之比等于
| V1 |
| V2 |
| 1 |
| 3 |
| 1 |
| 27 |
故答案为:
| 1 |
| 27 |


练习册系列答案
相关题目
 的函数
的函数 ,若同时满足:①
,若同时满足:① 在
在
 ,使
,使 上的值域为
上的值域为 )叫做闭函数.
)叫做闭函数. 符合条件②的区间
符合条件②的区间 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.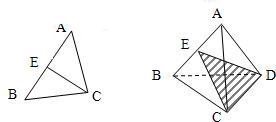

 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是 ,若
,若 则
则 的所有可能值为( )
的所有可能值为( )


