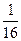题目内容
在平面几何中，△ABC的内角平分线CE分AB所成线段的比为
=
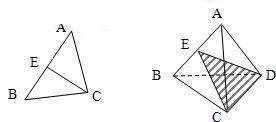
，把这个结论类比到空间：在正三棱锥A-BCD中（如图所示），平面DEC平分二面角A-CD-B且与AB相交于E，则得到的类比的结论是______．
| AE |
| EB |
| AC |
| BC |
在△ABC中作ED⊥AC于D，EF⊥BC于F，则ED=EF，∴
=
=
根据面积类比体积，长度类比面积可得：
=
故答案为：
=
| AC |
| BC |
| S△AEC |
| S△BCE |
| AE |
| EB |
根据面积类比体积，长度类比面积可得：
| V△A-CDE |
| V△B-CDE |
| S△ACD |
| S△BCD |
故答案为：
| V△A-CDE |
| V△B-CDE |
| S△ACD |
| S△BCD |
练习册系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
中，猜想
的最大值，并证明之。
在点
处的导数是 ( )
