题目内容
【题目】（本小题满分10分）选修4—5：不等式选讲
设函数f（x）=|2x﹣7|+1．
（Ⅰ）求不等式f（x）≤x的解集；
（Ⅱ）若存在x使不等式f（x）﹣2|x﹣1|≤a成立，求实数a的取值范围．
【答案】（Ⅰ）
（Ⅱ）
【解析】试题分析：根据零点分区间讨论法解绝对值不等式，存在
使不等式
成立，只需研究函数
，分区间化简函数，求出函数
的最小值，得出
的范围.
试题解析：
（Ⅰ）由f（x）≤x得|2x﹣7|+1≤x，
∴
，
∴不等式f（x）≤x的解集为
；
（Ⅱ）令g（x）=f（x）﹣2|x﹣1|=|2x﹣7|﹣2|x﹣1|+1，
则
，∴g（x）min=﹣4，
∵存在x使不等式f（x）﹣2|x﹣1|≤a成立，
∴g（x）min≤a，∴a≥﹣4．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】利民奶牛场在2016年年初开始改进奶牛饲养方法，同时每月增加一定数目的产奶奶牛，2016年2到5月该奶牛场的产奶量如表所示：
月份 | 2 | 3 | 4 | 5 |
产奶量y（吨） | 2.5 | 3 | 4 | 4.5 |
（1）在给定的坐标系中画出表中数据的散点图；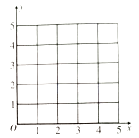 
（2）求出y关于x的线性回归方程；
（3）试预测该奶牛场6月份的产奶量？ （注：回归方程 
= 
x+ 
中， = 
= 
， = 
﹣ 
）
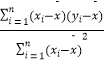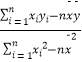