题目内容
【题目】(本小题满分12分)
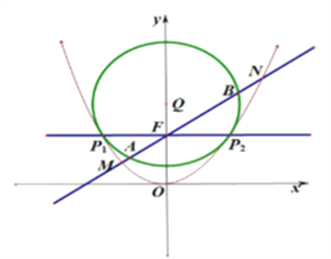
在直角坐标系中,已知![]() ,若
,若![]() 。
。
(Ⅰ)求动点P的轨迹![]() 的方程;
的方程;
(Ⅱ)过点M的直线![]() 与(1)中轨迹
与(1)中轨迹![]() 相交于点A、B,求
相交于点A、B,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:本题点![]() 满足到两个定点距离之和为定值,满足椭圆的定义,根据椭圆定义求出椭圆的标准方程,最值问题为解析几何常见考题,高考试题中经常可以看到它的身影,先合理表示三角形的面积,然后求最值,求最值有时使用基本不等式,有时还可以求导.
满足到两个定点距离之和为定值,满足椭圆的定义,根据椭圆定义求出椭圆的标准方程,最值问题为解析几何常见考题,高考试题中经常可以看到它的身影,先合理表示三角形的面积,然后求最值,求最值有时使用基本不等式,有时还可以求导.
试题解析:
(Ⅰ)由椭圆的定义可知,动点P的轨迹为以M、N为焦点的椭圆。
设![]() ,则
,则![]() 的方程为:
的方程为: ![]()
(Ⅱ)设![]() :
: ![]()
![]() 得
得![]()
设![]() ,则有
,则有 ![]()
所以 ![]()
![]()
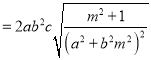 (
(![]() R)
R)
设![]() ,则有
,则有![]()
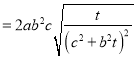
![]()
![]()
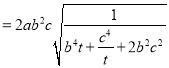 (
(![]() )
)
当![]() 即
即![]() 时,
时, ![]()
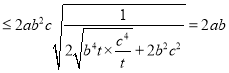
当且仅当![]() 时取等号,这时
时取等号,这时![]() 面积的最大值为
面积的最大值为![]() (其中
(其中![]() )
)
当![]() 即
即![]() 时,可证
时,可证![]() 在
在![]() 上为增函数,当
上为增函数,当![]() 时,
时,
u有最小值, ![]() 有最大值
有最大值![]() (其中
(其中![]() ).
).

练习册系列答案
相关题目