题目内容
11．设变量x，y满足约束条件：$\left\{\begin{array}{l}{x-y≤0}\\{x+2y≤3}\\{4x-y≥-6}\end{array}\right.$，则z=$\frac{{2}^{x}}{{4}^{y}}$的取值范围为[$\frac{1}{32}$，4]．分析 首先画出平面区域，将z变形，得到z=2x-2y，只要求出x-2y的最值即可．
解答 解：变量x，y满足约束条件：$\left\{\begin{array}{l}{x-y≤0}\\{x+2y≤3}\\{4x-y≥-6}\end{array}\right.$对应的平面区域如图：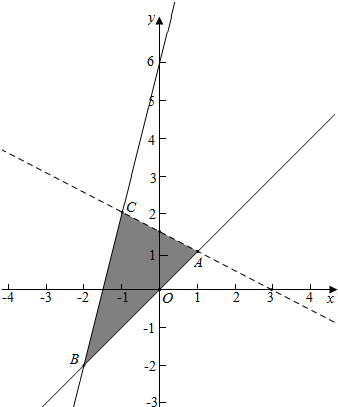
，
z=$\frac{{2}^{x}}{{4}^{y}}$=2x-2y，x-2y的最大值为过B时的值为-2-2（-2）=2，最小值为国C时的值为-1-2×2=-5，所以x-2y的取值范围为[-5，2]，z=$\frac{{2}^{x}}{{4}^{y}}$=2x-2y的取值范围为[$\frac{1}{32}$，4]．
点评 本题考查了简单线性规划问题的解答，运用了数形结合的数学思想．
练习册系列答案
名校课堂系列答案
相关题目
16．已知α，β是两个不同的平面，m，n是两条不同的直线，则下列命题不正确的是（ ）
| A． | 若α∥β，m?α，则m∥β | B． | 若m⊥α，n⊥α，n⊥β，则m⊥β | ||
| C． | 若m∥α，n∥β且α⊥β，则m⊥n | D． | 若α∥β，m⊥α，n∥β，则m⊥n |