Question

5．若不等式x²+1≥ax+b≥$\frac{3}{2}$x${\;}^{\frac{2}{3}}$对任意的x∈[0，+∞）恒成立．求实数b的取值范围以及a与b满足的关系式．

Answer 1

分析 分别画出函数y=x²+1，y=$\frac{3}{2}$x${\;}^{\frac{2}{3}}$在x∈[0，+∞）的图象，可得b的范围，讨论a的范围，①当a≤0时，②当a＞0时，由恒成立思想，结合导数判断单调性，求得最值，解不等式即可得到a，b的范围．

解答 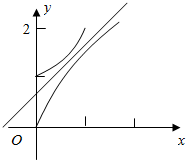解：分别画出函数y=x²+1，y=$\frac{3}{2}$x${\;}^{\frac{2}{3}}$在x∈[0，+∞）的图象，
可得y=ax+b的纵截距b的范围是（0，1），
①当a≤0时，
由x²+1-ax-b≥0恒成立，即为（x²+1-ax-b）_min≥0，
由f（x）=x²+1-ax-b的导数为f′（x）=2x-a≥0在[0，+∞）恒成立，
f（x）在[0，+∞）递增，
即有f（0）取得最小，且为1-b，即1-b≥0，解得b≤1，
又ax+b-$\frac{3}{2}$x${\;}^{\frac{2}{3}}$≥0恒成立，即为（ax+b-$\frac{3}{2}$x${\;}^{\frac{2}{3}}$）_min≥0，
由g（x）=ax+b-$\frac{3}{2}$x${\;}^{\frac{2}{3}}$的导数为a-${x}^{-\frac{1}{3}}$≤0，即g（x）在[0，+∞）递减，
则g（x）无最小值；
②当a＞0时，
由x²+1-ax-b≥0恒成立，即为（x²+1-ax-b）_min≥0，
由f（x）=x²+1-ax-b的导数为f′（x）=2x-a，
可得x=$\frac{1}{2}$a处导数左负右正，取得极小值，也为最小值1-b-$\frac{{a}^{2}}{4}$，
即1-b-$\frac{{a}^{2}}{4}$≥0，解得b≤1-$\frac{{a}^{2}}{4}$；
又ax+b-$\frac{3}{2}$x${\;}^{\frac{2}{3}}$≥0恒成立，即为（ax+b-$\frac{3}{2}$x${\;}^{\frac{2}{3}}$）_min≥0，
由g（x）=ax+b-$\frac{3}{2}$x${\;}^{\frac{2}{3}}$的导数为a-${x}^{-\frac{1}{3}}$，当x=a^-3时导数左负右正，
取得极小值，且为最小值b-$\frac{1}{2}$a^-2．即b-$\frac{1}{2}$a^-2≥0，解得b≥$\frac{1}{2}$a^-2．
综上可得b的范围是（0，1），a，b满足的条件为$\frac{1}{2}$a^-2≤b≤1-$\frac{{a}^{2}}{4}$．

点评 本题考查不等式的恒成立问题的解法，注意运用导数，判断单调性，求得最值，同时考查分类讨论的思想方法，属于中档题．