题目内容
20.已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:f(a•b)=af(b)+bf(a).(1)求f(0),f(1)的值;
(2)判断f(x)的奇偶性,并证明你的结论;
(3)若f(2)=2,g(n)=$\frac{f({2}^{-n})}{n}$(n∈N*),求g(n)的解析式.
分析 (1)赋值法,令a=b=0和令a=b=1,可分别求出f(0)、f(1)
(2)构造f(-x)和f(x)之间的关系式,看符合奇函数还是偶函数,先赋值求出f(-1),再令a=-1,b=x即可
(3)从而可知数列{$\frac{{A}_{n}}{{2}^{-n}}$}是以-1为,-1为首项的等差数列,故可求数列{An}的通项公式,从而得出数列g(n)的通项公式
解答 解:(1)令a=b=0,代入得f(0)=0•f(0)+0•f(0)=0.
令a=b=1,代入得f(1)=1•f(1)+1•f(1),则f(1)=0.
(2)∵f(1)=f[(-1)2]=-f(-1)-f(-1)=0,
∴f(-1)=0.
令a=-1,b=x,则f(-x)=f(-1•x)=-f(x)+xf(-1)=-f(x),
因此f(x)是奇函数.
(3)令a=2,b=$\frac{1}{2}$,得f(1)=2f($\frac{1}{2}$)+$\frac{1}{2}$f(2),且f(2)=2,
∴f($\frac{1}{2}$)=-$\frac{1}{2}$,
令a=2-n,b=2,得f(2-n+1)=2-nf(2)+2f(2-n)
设An=f(2-n)
∴An-1=2-(n-1)+2An,
∴$\frac{{A}_{n-1}}{{2}^{-(n-1)}}$=1+$\frac{{A}_{n}}{{2}^{-n}}$,
即$\frac{{A}_{n}}{{2}^{-n}}$-$\frac{{A}_{n-1}}{{2}^{-(n-1)}}$=-1,且$\frac{{A}_{1}}{\frac{1}{2}}$=$\frac{f(\frac{1}{2})}{\frac{1}{2}}$=-1,
即数列{$\frac{{A}_{n}}{{2}^{-n}}$}是以-1为,-1为首项的等差数列,
∴$\frac{{A}_{n}}{{2}^{-n}}$=-n,
∴An=-n•2-n
∴g(n)=-$\frac{1}{{2}^{n}}$.
点评 本题考查赋值法的巧妙使用、奇函数和偶函数的判定以及等差数列的证明和通项公式的求法,属中档题

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案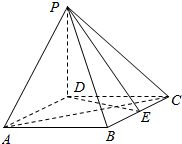 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.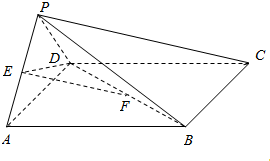 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.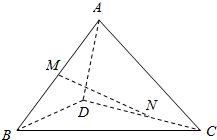 在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.
在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.