题目内容
14.若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数y=x2,x∈[1,2]与函数y=x2,x∈[-2,-1]即为“同族函数”.请你找出下面哪些函数解析式也能够被用来构造“同族函数”,答:①③⑤(请填写序号)①y=|x-2|; ②y=x; ③y=log${\;}_{\frac{1}{2}}$(1-x2); ④y=5x; ⑤y=$\frac{{2}^{-x}+{2}^{x}}{{x}^{2}}$.
分析 由题意能够被用来构造“同族函数”的函数必须满足在其定义域上不单调.逐个选项判断即可.
解答 解:由题意可得“同族函数”需对于同一函数值,有不同的自变量与之对应.
故能够被用来构造“同族函数”的函数必须满足在其定义域上不单调.
∵函数y=|x-2|在(-∞,2)上是减函数,在(2,+∞)上是增函数,
∴y=|x-2|能够被用来构造“同族函数”,故①正确;
∵函数y=x在(-∞,+∞)上是增函数,
∴y=x不能够被用来构造“同族函数”,故②不正确;
∵函数y=log${\;}_{\frac{1}{2}}$(1-x2)在(-1,0)上是减函数,在(0,1)上是增函数,
∴y=log${\;}_{\frac{1}{2}}$(1-x2)能够被用来构造“同族函数”,故③正确;
∵函数y=5x在(-∞,+∞)上是增函数,
∴y=5x不能够被用来构造“同族函数”,故④不正确;
∵函数y=$\frac{{2}^{-x}+{2}^{x}}{{x}^{2}}$在(-∞,0)上是减函数,在(0,+∞)上是增函数,
∴y=$\frac{{2}^{-x}+{2}^{x}}{{x}^{2}}$能够被用来构造“同族函数”,故⑤正确;
综上所述,能够被用来构造“同族函数”的函数有①③⑤
故答案为:①③⑤
点评 本题考查“同族函数”的定义,转化为基本初等函数的单调性是解决问题的关键,属中档题.

练习册系列答案
相关题目
4.点P在直线l:x-y-1=0上运动,A(4,1),B(2,0),则|PA|+|PB|的最小值是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 4 |
6.定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,f($\frac{x}{5}$)=$\frac{1}{2}f(x)$,且当0≤x1≤x2≤1时,f(x1)≤f(x2),则f($\frac{1}{2015}$)等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
 三角形ABC中,AD=DB,AG=2CG,BE=FC=$\frac{1}{4}$BC,四边形DEFG的面积占三角形ABC面积的几分之几?
三角形ABC中,AD=DB,AG=2CG,BE=FC=$\frac{1}{4}$BC,四边形DEFG的面积占三角形ABC面积的几分之几?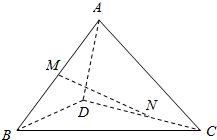 在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.
在空间四边形ABCD中,AC⊥BD,M、N分别是AB、CD的中点,AC=4,BD=3,求:MN和BD所成的角的正切值.